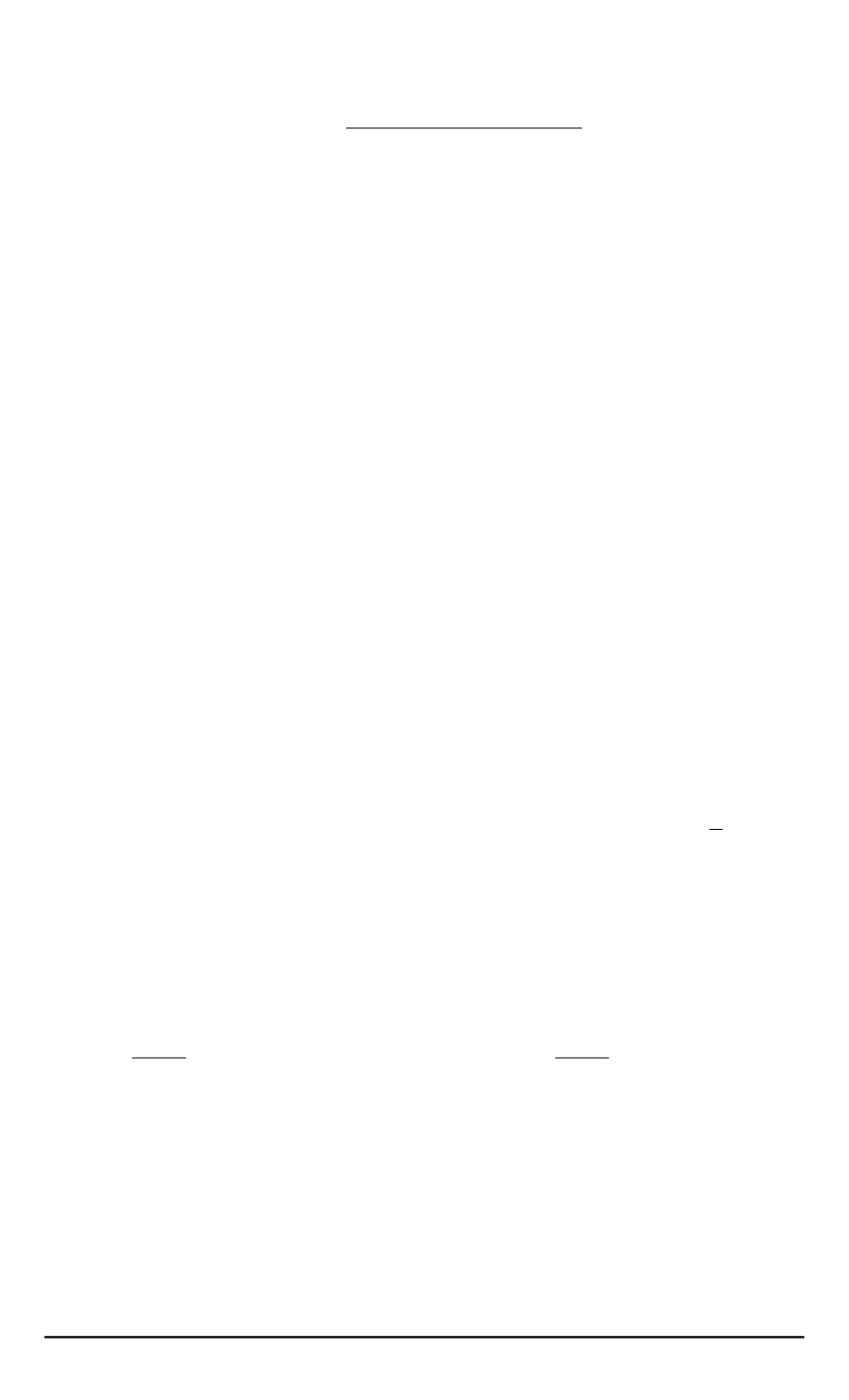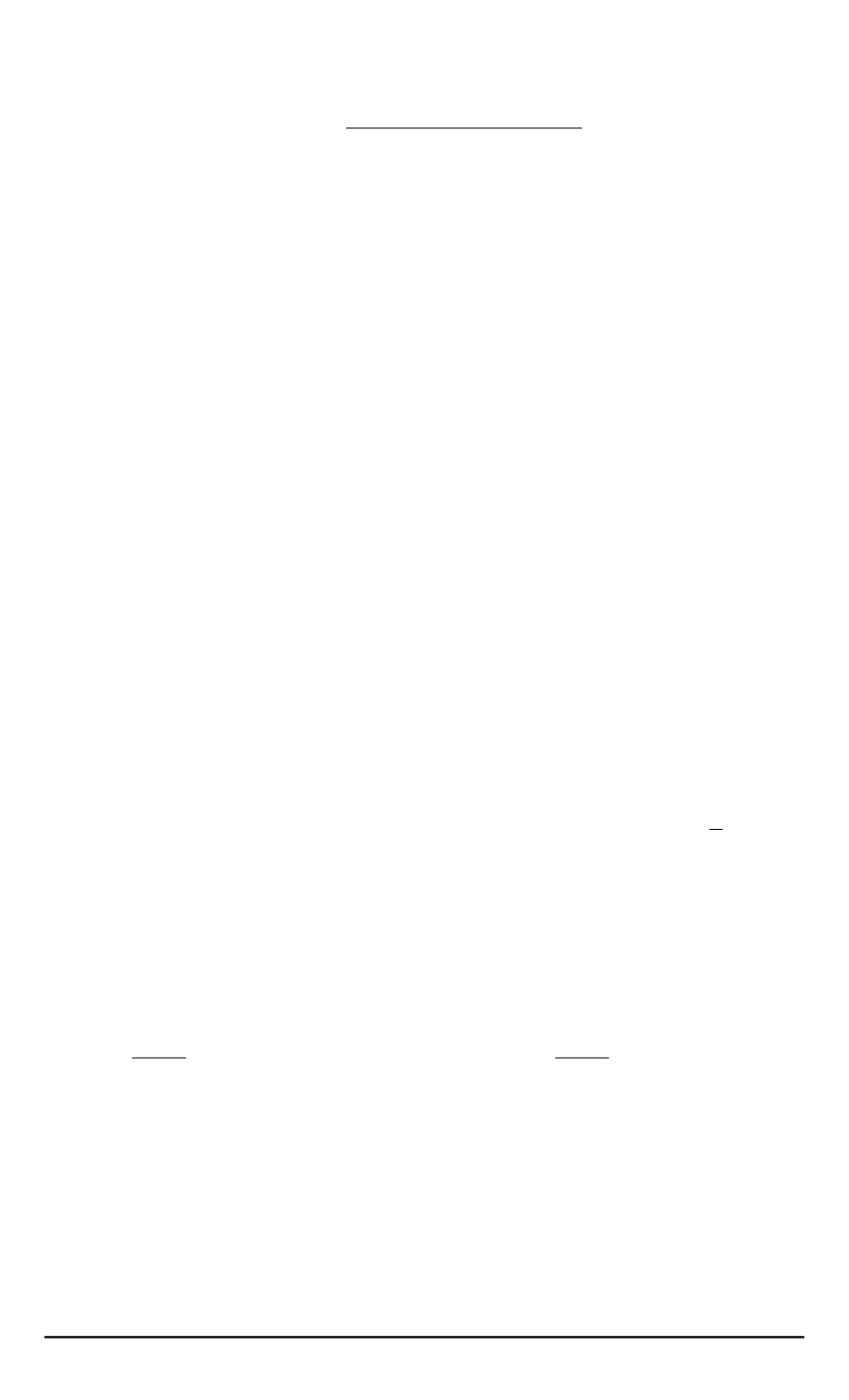
Для проверки
(1)
предлагается статистика вида
T
2
n
=
max
0
6
t
<
∞
S
2
n
(
t
) =
max
0
6
t
<
∞
b
P
Q
(
t
)
(
b
P
Q
(
t
))
2
+ (
1
−
b
P
Q
(
t
))
2
¯ ¯ ¯ b
P
Θ
(
t
)
−
b
P
Q
(
t
)
¯ ¯ ¯
.
(
3
)
Статистика
(3)
является аналогом статистики Смирнова примени
-
тельно к рассматриваемой проблеме
,
при этом с ее помощью проверя
-
ется однородность двух выборок
,
хотя они не являются независимыми
и
,
кроме того
,
одна из них
—
прогрессивно цензурируемая выборка
.
Точные распределения
.
Заметим
,
прежде всего
,
что распределе
-
ние статистики
(3)
не зависит от вида
F
0
(
t
)
,
так как значения
S
2
n
(
t
)
полностью определяются взаимным расположением элементов выбор
-
ки
Q
,
т
.
е
.
распределение инвариантно относительно любого монотон
-
но возрастающего преобразования
.
Будем в дальнейшем считать
,
что
F
0
(
t
) =
t
, 0
≤
t
≤
1.
Отсюда следует
,
что маргинальные распределения
величин
θ
i
,
η
i
равны
F
θ
(
t
) =
2
t
−
t
2
,
F
η
(
t
) =
t
2
, 0
6
t
6
1.
Пусть
v
1
<
v
2
< . . . <
v
2
n
—
вариационный ряд выборки
Q
,
z
i
=
(
1
,
если
v
i
—
один из минимумов
,
0
,
если
v
i
—
один из максимумов
,
v
i
=
i
∑
j
=
1
z
j
,
i
=
1
,
2
, . . . ,
2
n
.
Вектор
z
=
¡
z
1
,
z
2
, . . . ,
z
2
n
¢
будем называть допустимым
,
если он
состоит из
n
нулей и
n
единиц и выполняются неравенства
i
2
6
v
i
6
6
min
(
i
,
n
)
,
i
=
1
,
2
, . . . ,
2
n
.
Очевидно
,
что результатом эксперимента
могут быть только допустимые векторы
.
В работе
[5]
доказана следу
-
ющая лемма
.
Лемма
1
.
При справедливости равенства
(1)
распределение векто
-
ра
z
имеет вид
p
(
z
) =
2
n
n
!
(
2
n
)
!
¡
r
1
−
1
¢ ¡
r
2
−
3
¢
. . .
(
r
n
−
2
n
+
1
) =
2
n
n
!
(
2
n
)
!
n
∏
j
=
1
³
r
j
−
2
j
+
1
´
,
где
r
j
—
номер
(
ранг
) j-
го нуля в
z,
2
≤
r
1
<
r
2
<
· · ·
<
r
n
=
2
n.
Чтобы найти точное распределение статистики
(3),
рассмотрим сле
-
дующую модель случайного блуждания
.
Пусть
n
a
i j
o
=
A
,
i
=
0
,
1
, . . . ,
n
,
j
=
0
,
1
, . . . ,
i
, —
двумерный мас
-
сив ячеек
(
имеющий треугольный вид
).
Частица начинает блуждание из
ячейки
a
00
и на
k
-
м шаге переходит из
a
v
k
−
1
,
k
−
1
−
v
k
−
1
в ячейку
a
v
k
,
k
−
v
k
−
1
.
30 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2003.
№
2