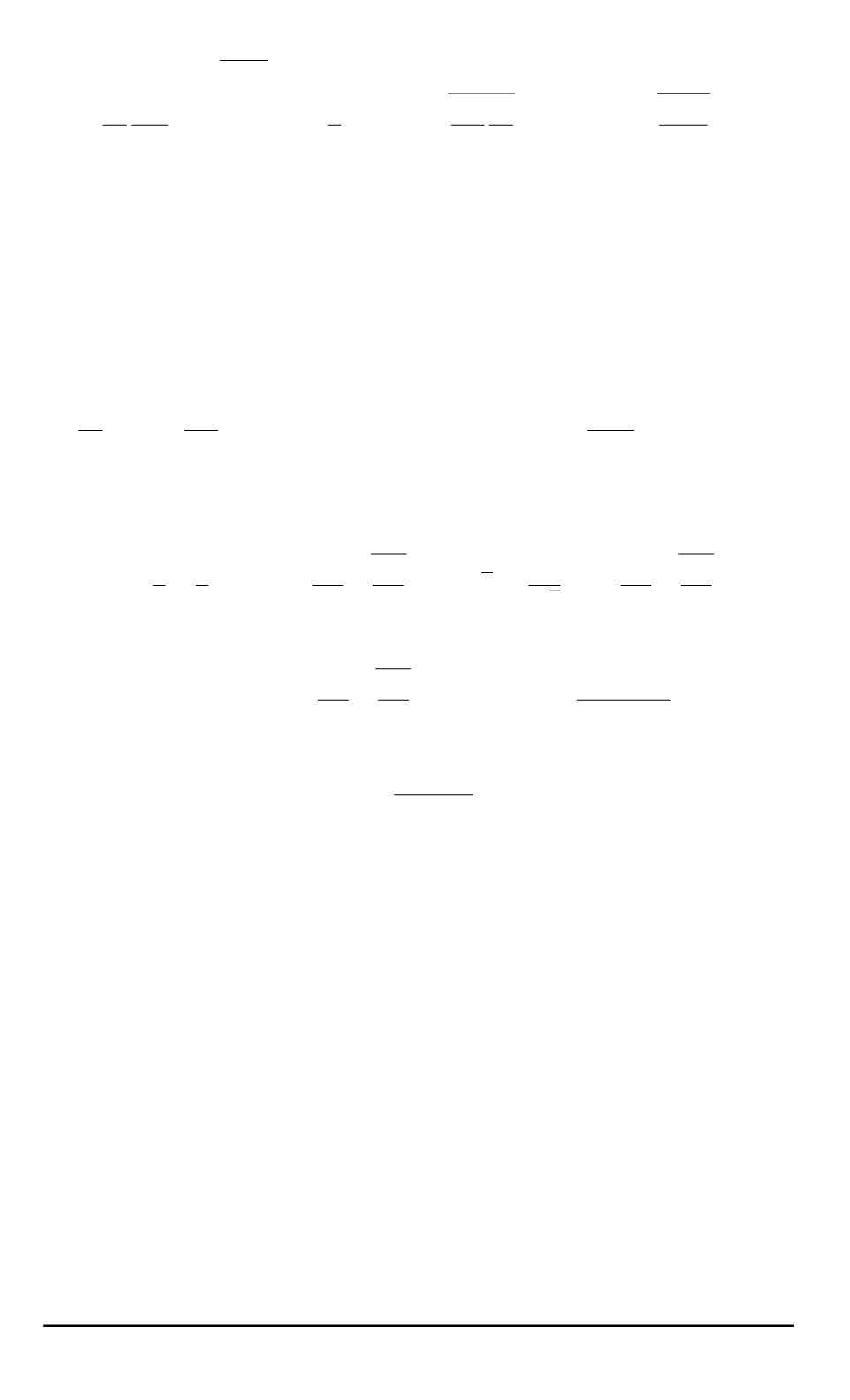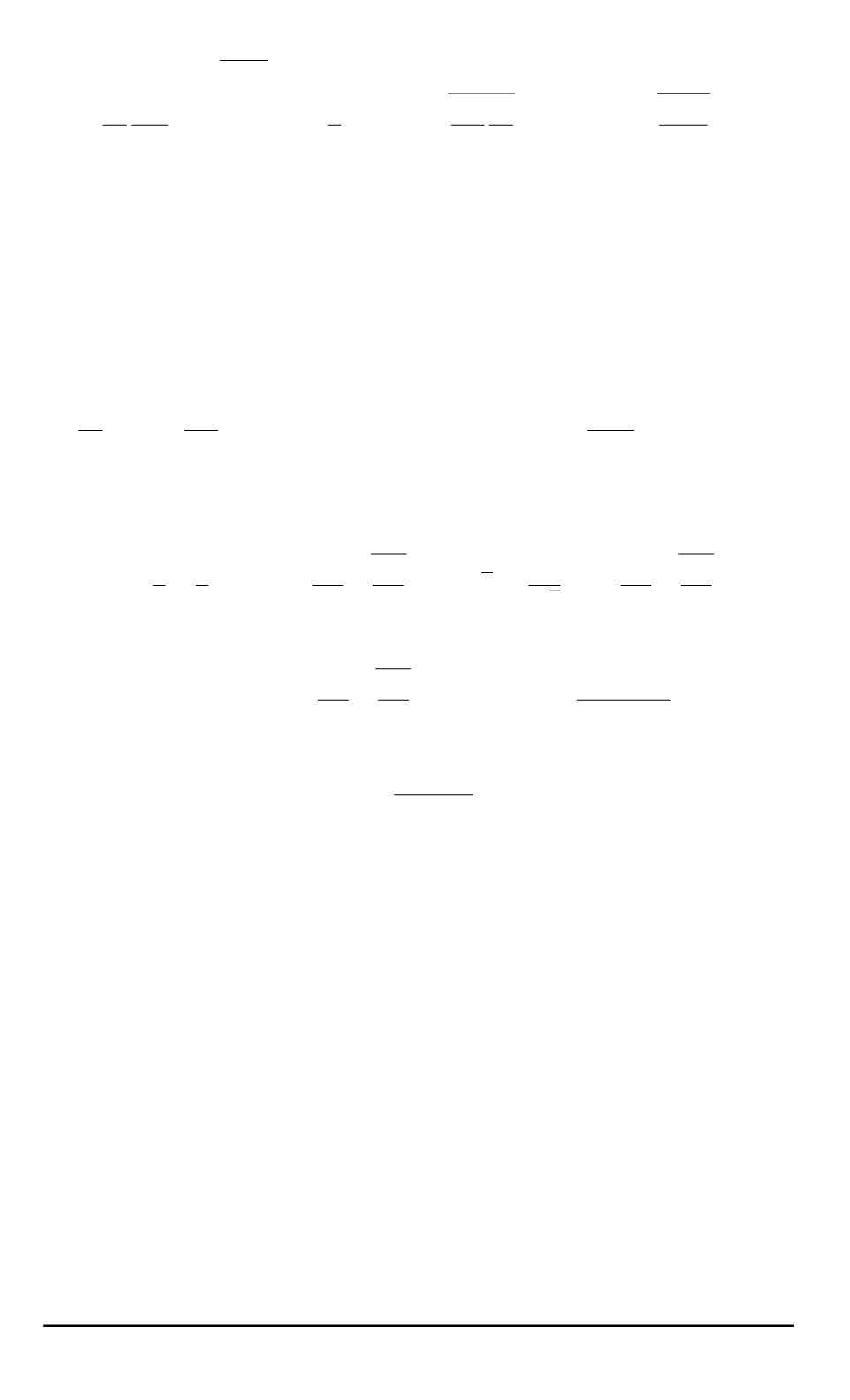
z
= 1
, J
e
=
n
e
w
i
2
, n
n
= 0
, T
=
T
w
,
−
λ
e
R
dT
e
dz
=
−
n
e
w
i
kT
e
µ
1
2
+ ln
µ
2
r
m
e
m
h
T
T
e
¶¶
, w
i
=
r
8
kT
πm
h
,
(
37
)
где
w
i
—
скорость ионов
;
T
w
—
температура тяжелых частиц на стенке
.
Скорости неупругих процессов возбуждения уровней и ионизации
,
обратных процессов дезактивации и рекомбинации рассчитываются
путем свертки функций распределения с соответствующими сечения
-
ми
.
При этом изотропная часть
f
0
функции распределения электронов
рассчитывается из уравнения Больцмана
,
которое в данном случае име
-
ет вид
[3]
ε
d
dε
µ
εa
(
ε
)
df
0
dε
(
ε
) +
b
(
ε
)
f
0
(
ε
)
¶
=
−
(
ε
)
µ
f
0
(
ε
)
−
g
0
n
1
g
1
n
0
f
0
(
ε
−
ε
01
)
¶
,
(
38
)
где
a
(
ε
) =
2
3
1
ε
ε
Z
0
εf
0
(
ε
)
4
π
m
e
r
2
ε
m
e
dε
+
√
ε
∞
Z
ε
1
√
ε
f
0
(
ε
)
4
π
m
e
r
2
ε
m
e
dε
,
b
(
ε
) =
ε
Z
0
f
0
(
ε
)
4
π
m
e
r
2
ε
m
e
dε,
−
(
ε
) =
ε
2
n
0
Q
01
(
ε
)
n
e
m
2
e
Γ
ee
,
Γ
ee
= 4
π
µ
e
2
4
πε
0
m
e
¶
2
ln Λ
,
ε
—
энергия электронов
;
ε
01
—
энергия резонансного уровня
;
ln Λ
—
кулоновский логарифм
[3];
n
0
и
n
1
—
концентрации частиц излучаю
-
щего компонента на основном и резонансном уровнях соответствен
-
но
;
g
0
и
g
1
—
статистические веса основного и резонансного уровней
соответственно
;
Q
01
(
ε
)
—
сечение возбуждения резонансного уровня
.
Видно
,
что коэффициенты
a
(
ε
)
,
b
(
ε
)
являются фукционалами функции
распределения
.
В качестве параметров в уравнении
(38)
присутствуют
величины
n
0
,
n
1
,
n
e
.
В работе
[3]
предполагается
,
что средняя энергия электронов на
-
много меньше энергии резонансного уровня
ε
01
,
тогда основной вклад в
интеграл неупругих столкновений вносят переходы между основным и
резонансным уровнями
,
причем учитывается влияние неупругих столк
-
новений только для электронов
,
энергия которых больше энергии
ε
01
.
В уравнение
(38)
в качестве параметров входят температура и кон
-
центрация электронов
,
а также заселенности основного и резонансного
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
4
59