а выражение
(25)
принимает вид
θ
=
Z
∆
ν
p
10
(
ν
)
m
I
1
(
x
1
ν
)
s
k
0
ν
3
k
0
ν
Σ
+
mI
0
(
x
1
ν
)
I
0
(
x
ν
)
dν,
где
x
ν
=
s
3
k
0
ν
k
0
ν
Σ
k
0
ν
Σ
r, x
1
ν
=
s
3
k
0
ν
k
0
ν
Σ
k
0
ν
Σ
R.
Некоторые результаты расчета параметра
θ
на оси цилиндра в зави
-
симости от безразмерной радиальной координаты
z
=
r/R
,
получен
-
ные прямым интегрированием согласно выражению
(21)
и в диффузи
-
онном приближении
(23), (24),
в сравнении с данными работ
[5, 23–25]
представлены на рис
. 1, 2.
Данные получены при постоянном по ради
-
усу коэффициенте поглощения
,
чтобы можно было провести сопоста
-
вление с данными указанных работ
.
Прежде всего
,
отметим
,
что значе
-
ния параметра
θ
,
найденные прямым интегрированием и в диффузион
-
ном приближении
,
хорошо согласуются между собой и с результатами
указанных работ
.
Видно
,
что параметр
θ
сильно уменьшается с возра
-
станием коэффициента поглощения
.
Расхождение полученных данных
с данными работ
[5, 23, 24]
при малой оптической плотности
(
см
.
рис
. 1)
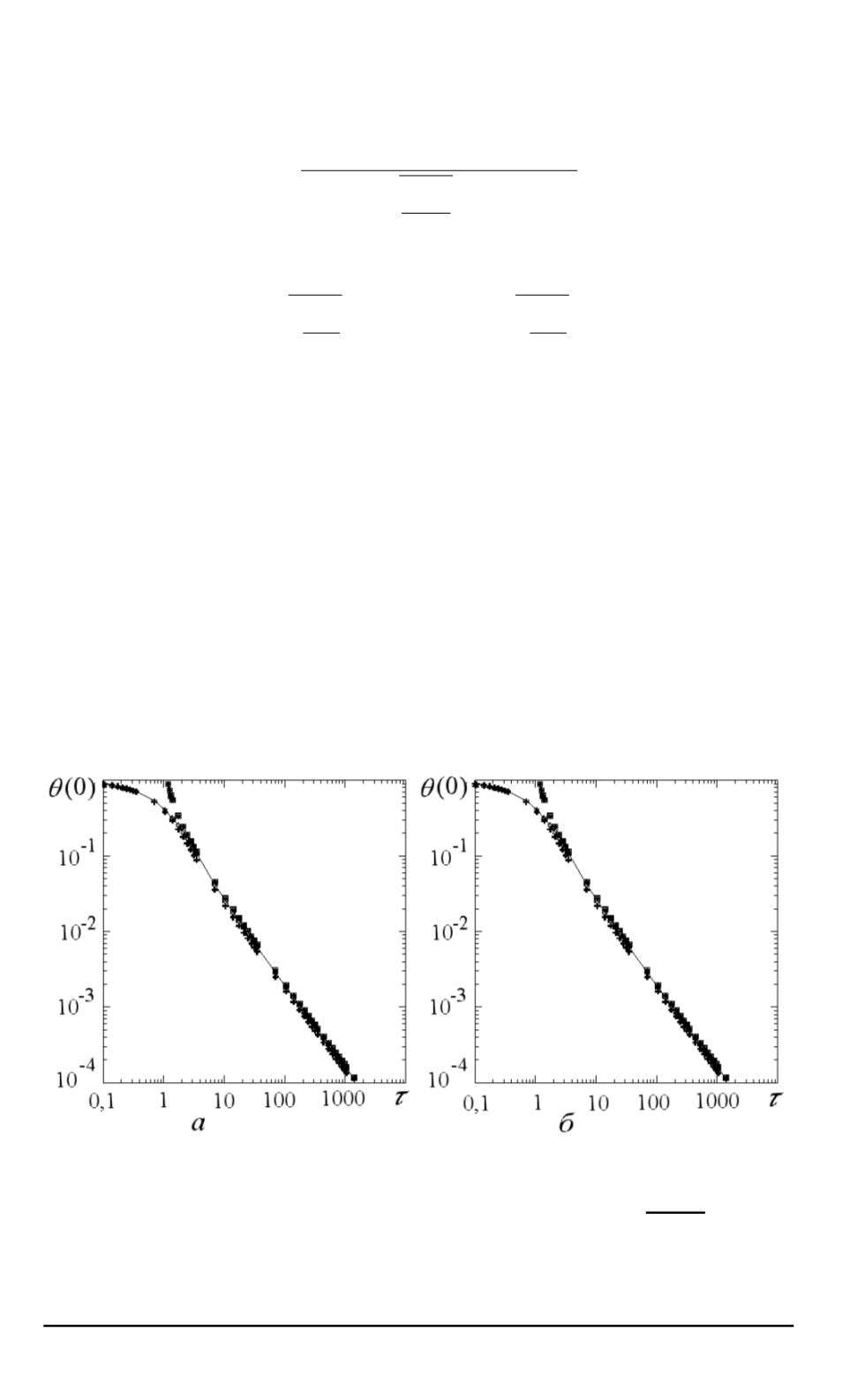
Рис
. 1.
Зависимость вероятности вылета фотона на оси цилиндра от оптической
плотности плазмы при радиусе цилиндра
R
= 0
,
35
см
:
а
—
доплеровский контур линии
,
б
—
лоренцевский контур линии
;
—
расчет
прямым интегрированием по формуле
(21);
+
—
расчет в рамках диффузионного при
-
ближения
(23), (24);
♦
—
данные работы
[5];
¤
—
данные работы
[23];
•
—
данные
работы
[24];
F
—
данные работы
[25]
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
4
53


