
Введение.
Классическими, разработанные в 1950–1970 гг. и ис-
пользуемые в настоящее время, стали методы регулирования частоты
вращения роторов паровых энергетических турбин, которые основаны
на простых и надежных алгоритмах, реализующих П- и ПД-принципы
регулирования. Подобные принципы используются, например, в тур-
бинах малой мощности, выпускаемых ОАО “Калужский турбинный
завод” (КТЗ) [1]. Указанные турбины просты в эксплуатации и ре-
монте гидромеханических регуляторов турбин, а также обеспечивают
требования стандарта [2, 3]. Если необходимые требования по частоте
вращения ротора турбогенератора по каким-либо причинам не выпол-
няются, то это не является критичным, поскольку турбогенераторы,
как правило, работают на некоторую сеть и частота вращения турби-
ны определяется частотой сети, так как турбогенераторы представля-
ют собой синхронные машины.
Для изолированно работающих энергосистем, где турбогенератор
работает на автономную нагрузку, требования по точности поддержа-
ния необходимой частоты вращения ротора турбины становятся доста-
точно жесткими, поскольку турбина может эксплуатироваться в ши-
роком диапазоне значений параметров острого пара и электрической
нагрузки.
В качестве примера рассмотрим структурную схему системы регу-
лирования частоты вращения ротора паровой энергетической турбины
ПТ-25/30-90/10М (рис. 1), выпускаемой КТЗ.
Относительные изменения понимаются в формате
(
x
текущее
−
x
ном
)
/x
ном
. Нелинейная характеристика имеет вид
F
(
z
) =
0
,
5
z
2
Δ
z
0
sign
z
при
|
z
| ≤
Δ
z
0
;
z
−
0
,
5Δ
z
0
sign
z
при
||
>
Δ
z
0
,
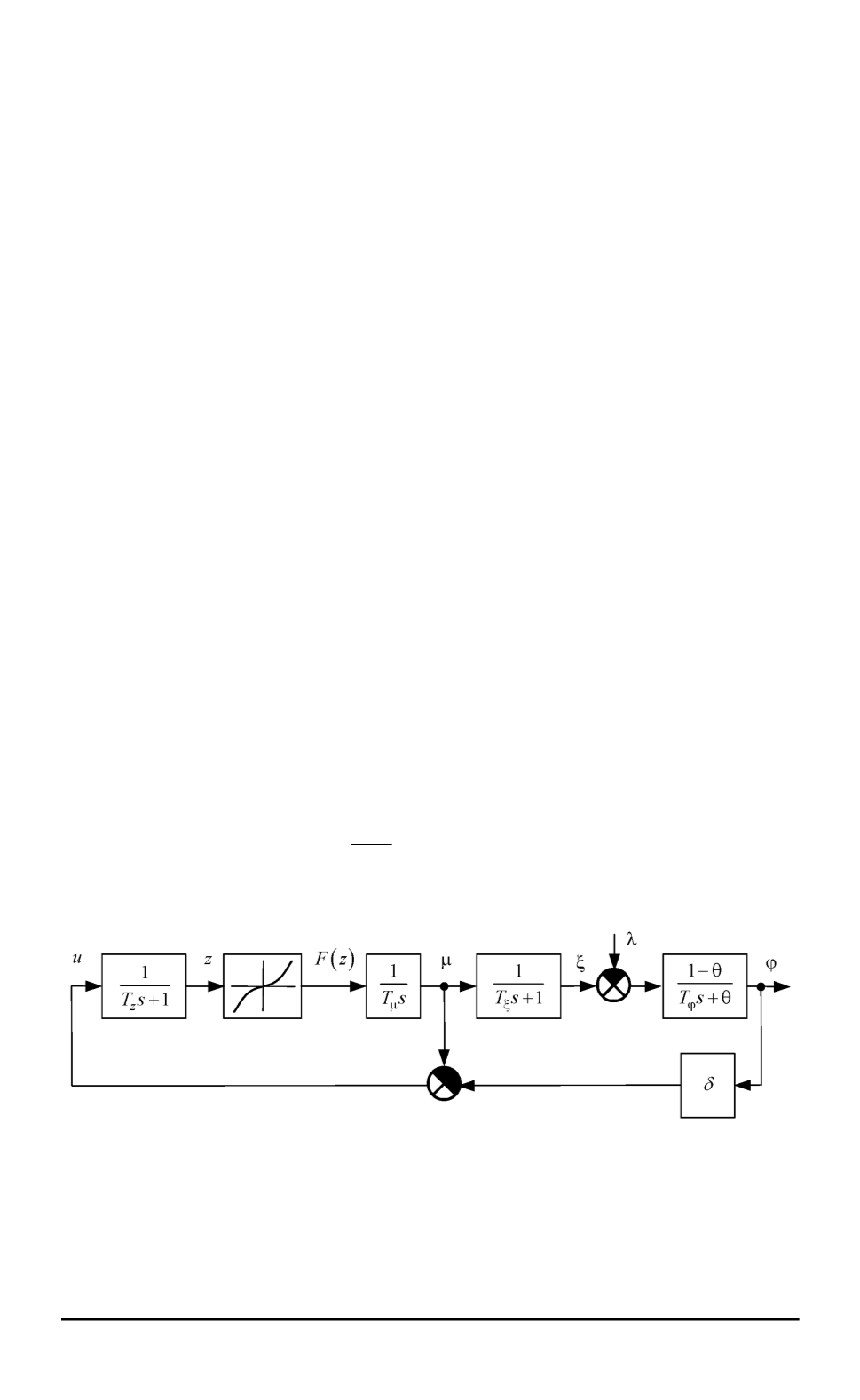
Рис. 1. Структурная схема системы регулирования частоты вращения ротора
турбины:
ϕ
,
ξ
,
μ
,
z λ
— относительные изменения частоты вращения ротора турбины, расхода
пара в турбине, отклонение поршня сервомотора, отклонение поршня золотника
и отклонение электрической нагрузки генератора;
T
z
, T
μ
, T
ξ
, T
ϕ
— постоянные
времени соответствующих элементов;
δ
— степень неравномерности системы
регулирования;
θ
— эквивалентный коэффициент самовыравнивания турбины
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 5
101
















