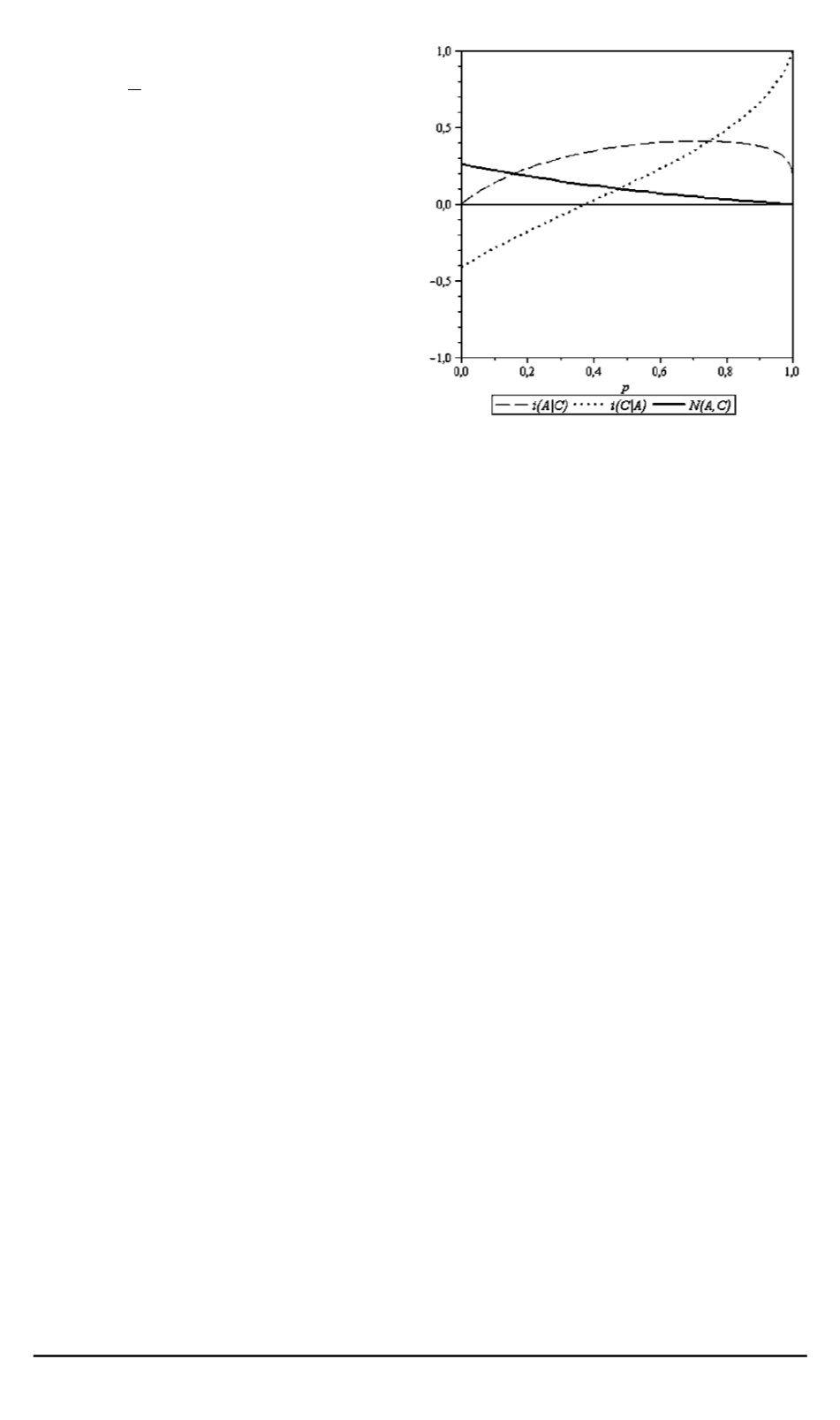
Рис. 9. Зависимость
i
и
N
от степени
диссипации
p
частицы
A
для редуциро-
ванной матрицы плотности
ρ
(
AC
)
со-
стояния (14)
На рис. 8,
в
видно, что на ин-
тервале
1
2
< p <
1
звено
A
−
BC
классически коррелировано (обе
i
положительны, в отличие от
рис. 5,
в
), но запутано. Анало-
гичная ситуация наблюдает на
рис. 8,
г
при
p >
0
,
625
для звена
AC
−
B
. Подсистема
AC
(рис. 9)
классически коррелирована и при
этом запутана, но на более широ-
ком интервале
0
,
375
< p <
1
.
Выводы 1–4,
сделанные
для диссипированного CKW-
состояния остаются справедли-
выми для WRr-состояния (с уче-
том меньшего значения
p
= 0
,
390
в количественной формулировке последнего вывода).
4. Заключение.
Классический причинный анализ, имеющий уже
богатую историю применения, дает две эквивалентные меры причин-
ности. Одна из них, ход времени
c
2
, оказывается применимой на кван-
товом уровне. Направление причинной связи находится как напра-
вление необратимого потока информации, определяемое знаком
c
2
;
количественная мера этой связи определяется модулем
c
2
: отсутствие
причинности соответствует
|
c
2
| → ∞
, т.е. чем меньше
|
c
2
|
, тем сильнее
причинность. Это формальное определение причинности справедливо
при любом направлении времени.
Возможности применения причинного анализа были продемон-
стрированы на серии примеров трехкубитных состояний. Примеры
упорядочены согласно степени возрастания асимметрии. Вычислен-
ные параметры причинности сравнивались со степенями смешанно-
сти и запутанности. В простейшем случае результаты формального
причинного анализа соответствуют ожидаемым, но уже при малом
усложнении квантовой системы интуиция не срабатывает. Таким обра-
зом, его применение ведет к нетривиальным следствиям относительно
распространения квантовой информации.
Зайковский и Городецкие [14] впервые поставили вопрос об осо-
бенностях передачи квантовой информации в асимметричных систе-
мах в зависимости от ее направления. Именно решению этого вопроса
и посвящена данная статья. По сравнению с первой работой по кван-
товому причинному анализу [4, 5], где рассматриваются лишь про-
стые двухкубитные состояния, в данной статье мы продемонстрирова-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3
105


