
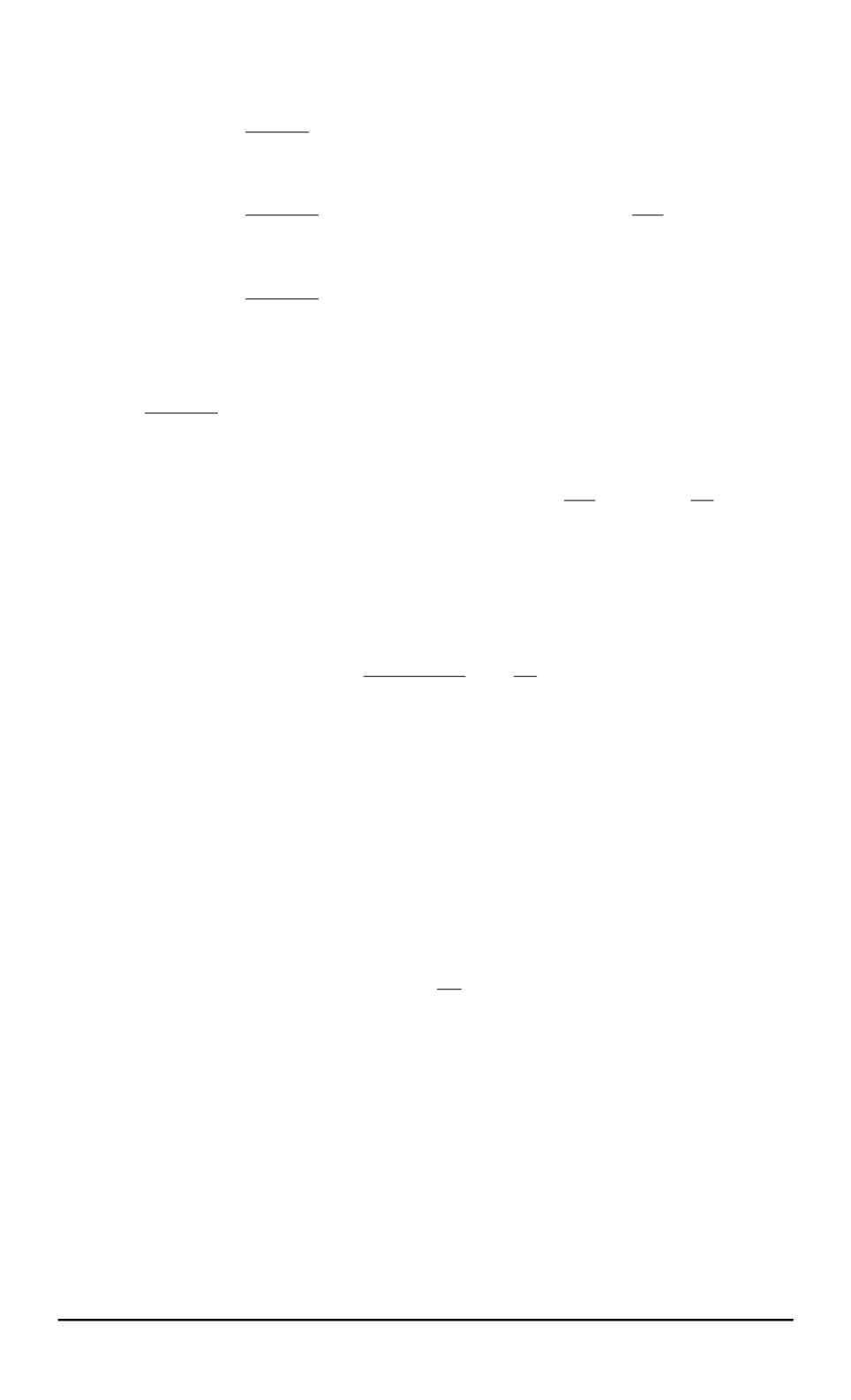
распределения флуктуаций скорости броуновской частицы
D
1
=
∂g
(
λ
)
i∂λ
λ
=0
= 0;
D
2
=
∂
2
g
(
λ
)
(
i∂λ
)
2
λ
=0
=
ν
τ
D
ξ
t
Z
−∞
G
2
(
t, τ
)
dτ
=
kT
m
;
D
3
=
∂
3
g
(
λ
)
(
i∂λ
)
3
λ
=0
= 0;
(4)
D
4
=
∂
4
g
(
λ
)
(
i∂λ
)
4
λ
=0
= 3
ν
2
τ
D
2
ξ
t
Z
−∞
G
2
(
t, τ
)
dτ
2
+
t
Z
−∞
G
4
(
t, τ
)
dτ
=
= 3
kT
m
2
1 +
γ
0
ν
τ
,
(5)
где
G
(
t, τ
)
— функция, определяемая по (2).
Формулы для моментов
D
2
(4) и
D
4
(5) позволяют рассчитать экс-
цесс функции распределения
κ
4
=
D
4
−
3
D
2
2
D
2
2
= 3
γ
0
ν
τ
,
(6)
выражение для которого совпадает с выражением, полученным в ра-
боте [7].
Для экспериментального определения интенсивности пуассонов-
ского процесса
ν
τ
может быть использована электролитическая ячей-
ка, описанная в работах [8–10]. Как показано в работе [10], экспери-
ментально наблюдаются долговременные изменения меры Кульбака
H
флуктуаций напряжения на электролитической ячейке, которая, в
свою очередь [7], связана с эксцессом простым соотношением
H
=
κ
4
16
.
(7)
При расчете эксцесса функции распределения флуктуаций напря-
жения
U
на электролитической ячейке необходимо учитывать, что эти
флуктуации возникают вследствие броуновского движения достаточ-
но большого числа ионов в малом объеме электролита, находящего-
ся в отверстиях в тонкой пленке, которая разделяет сосуды электро-
литической ячейки [8, 10]. Кроме того, необходимо учесть низкоча-
стотную фильтрацию флуктуаций напряжения, связанную с наличием
собственной электрической емкости электролитической ячейки. Для
описания флуктуаций напряжения вместо уравнения (1) необходимо
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 1
29
















