
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
89
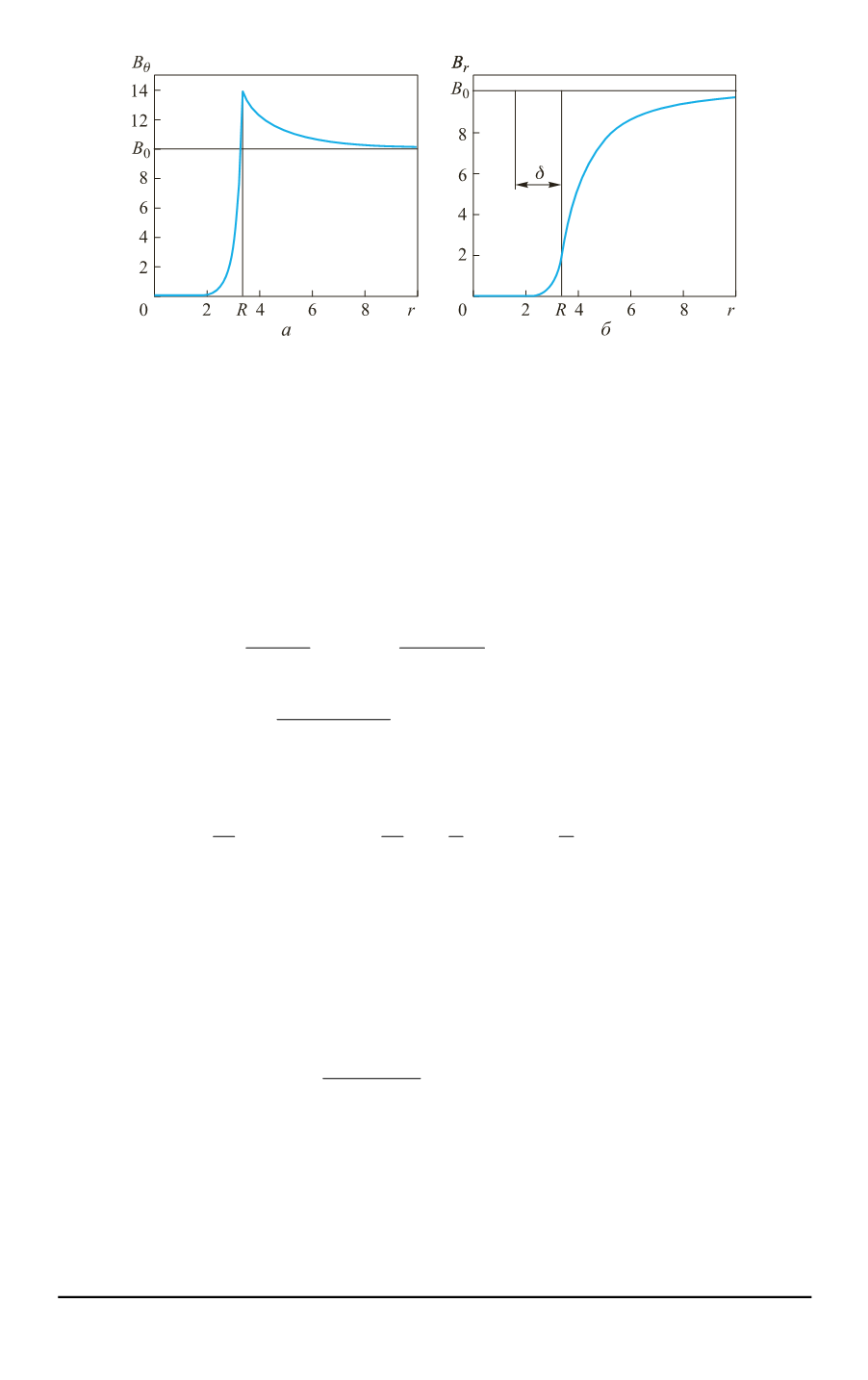
Рис. 1.
Зависимости компонент
B
(
а
) и
r
B
(
б
) магнитной
индукции от радиуса
r
в экваториальной плоскости сферы (при
θ = π/2) и на оси, проходящей через центр сферы параллельно
направлению внешнего магнитного поля (ось
z
, при
0)
Последний переход осуществлен с помощью второго уравнения
системы (7). Таким образом, отлична от нуля только компонента
j
вектора плотности тока сверхпроводящих электронов. Используя пер-
вое уравнение системы (8) и второе уравнение системы (9), получаем
2
2 2
0
0
0
2
0
sin
sh
ch sin
2
2
3
sh
ch sin .
2 sh
rf
D
j r
r r r
r
B R
r r r
r
R
Проверим на регулярность полученный результат
3
2
2
2
1
1 1
1
sh ch
1
0.
6
2
j
t t t
t
t t
t
t
t
t
Зависимость
j r
представлена на рис. 2. Ввиду того, что все ве-
личины очень быстро убывают на расстояниях около
4
10
см (при
1...10
R
см) зависимости, приведенные в настоящей работе, имеют
приблизительный вид.
Для оценки глубины проникания поверхностных токов
необхо-
димо решить уравнение
,
j R
e
j R
аналитическое решение которо-
го затруднительно вследствие крайней малости параметра задачи
4
/
10 .
R
Однако эта глубина по порядку величины должна быть та-
кая же, как и глубина, полученная в теории Лондонов. Тогда с учетом
изложенного работе [3] можно сформулировать основной физический
вывод полученного результата: во внешнем магнитном поле возникают
















