
Применение двойного квантования в диамагнетизме Ландау
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4
21
Заменим переменную интегрирования
p
переменной
/ 2,
p q
тогда инте-
грал примет простой симметричный вид
2
2
3 3
2
2
,
.
2
,
F
F
qp p
qp p
p p A q
e n
e
j q
A q
dp
m
m
p q
(20)
Соотношение (20) для удобства анализа представим как
( )
( ),
j q K A q
где
2
2
3 3
2
2
.
2
,
F
F
qp p
qp p
p p
e n
e
K
dp
m m
p q
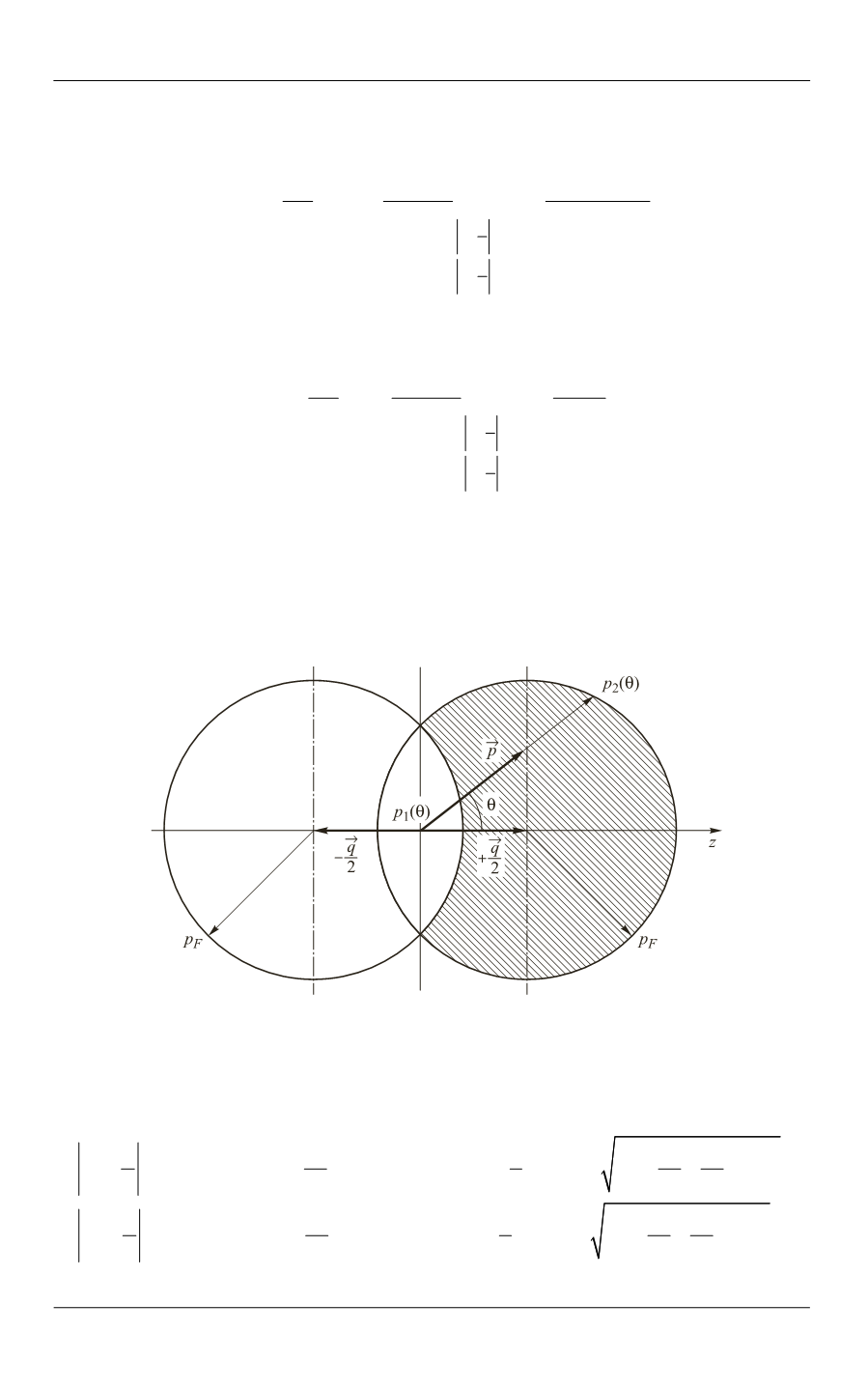
Интегрирование проводим в сферических координатах, учитывая, что зада-
ча имеет явно выраженный осесимметричный характер. Согласно приведенной
на рисунке схеме, полярный угол
изменяется в диапазоне значений
0... / 2,
азимутальный угол
— в диапазоне
0...2 ,
причем полярный угол — угол
между векторами
p
и
,
q
поэтому
,
cos .
p q pq
Схема области интегрирования в импульсном пространстве
Модуль вектора
p
изменяется в пределах
1
p
…
2
,
p
которые находят
как
2
2 2
2
2
2
2
1
1
1
1
2
2 2
2
2
2
2
2
2
2
2
1
;
cos ;
cos
cos ;
2
4
2
4 4
1
;
cos ;
cos
cos .
2
4
2
4 4
F
F
F
F
F
F
q
q
q q
p
p p p
p q
p
q
p
q
q
q q
p
p p p
p q
p q
p
















