
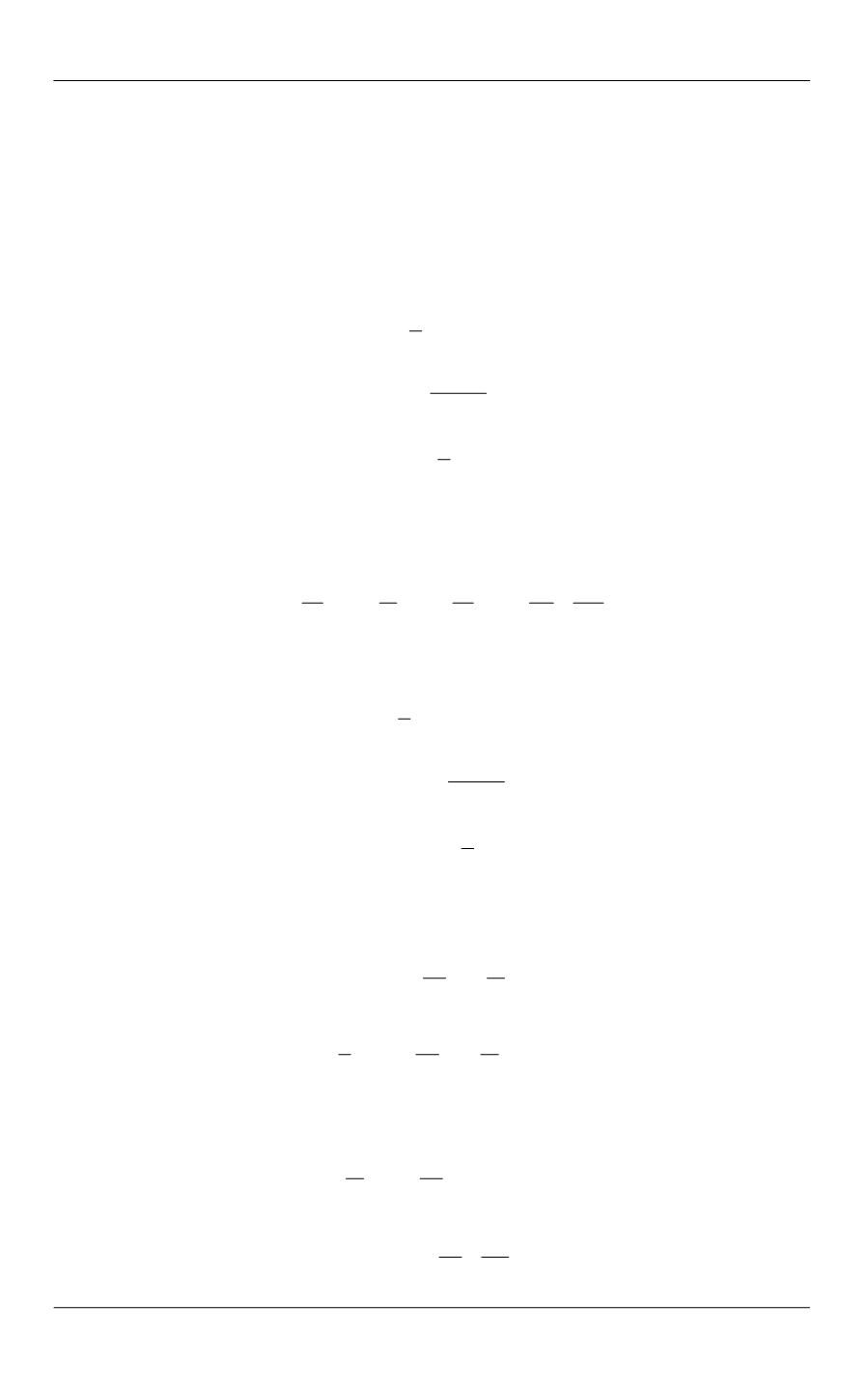
Гравитационные волны в конформно-плоских пространствах
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4
67
Уравнение динамики скалярного поля.
Запишем метрику пространствен-
но плоской Вселенной Фридмана — Робертсона — Уокера (ФРУ) в системе еди-
ниц
8 = =1:
G c
2
2
2
1 2
2 2
3 2
= ( )[
( ) ( ) ( ) ].
ds a t dt
dx
dx
dx
Уравнения динамики скалярного поля для плоской Вселенной ФРУ имеют
вид [4]
2
2
1 3 =
( );
2
H
V
(1)
( )
3
= 0;
dV H
d
(2)
2
1 = ,
2
H
(3)
где
= /
H a a
— параметр Хаббла;
— скалярное поле;
( )
V
— потенциал;
a
—
масштабный фактор. В терминах конформного времени
и с учетом
2
2
2
'
= ,
= ,
= ,
=
dt
a
d
H H
a
a
a
a a
преобразуем уравнения (1)–(3) к виду
2
2 2
1 3 =
( );
2
a V
(4)
2
( )
2
= 0;
dV a
d
2
2
1
'
= .
2
(5)
Здесь и далее знак «
'
» обозначает производную по конформному времени.
Из уравнения (5) получим
2
2
'
= 2
;
a
a
a a
2
2
1 = 2
.
2
a
a
a a
(6)
Подставим (6) в уравнение (4) и запишем
2
2
=
( );
a
a a V
a
a
2
3
4
( ( )) =
.
a a
V
a a
(7)
















