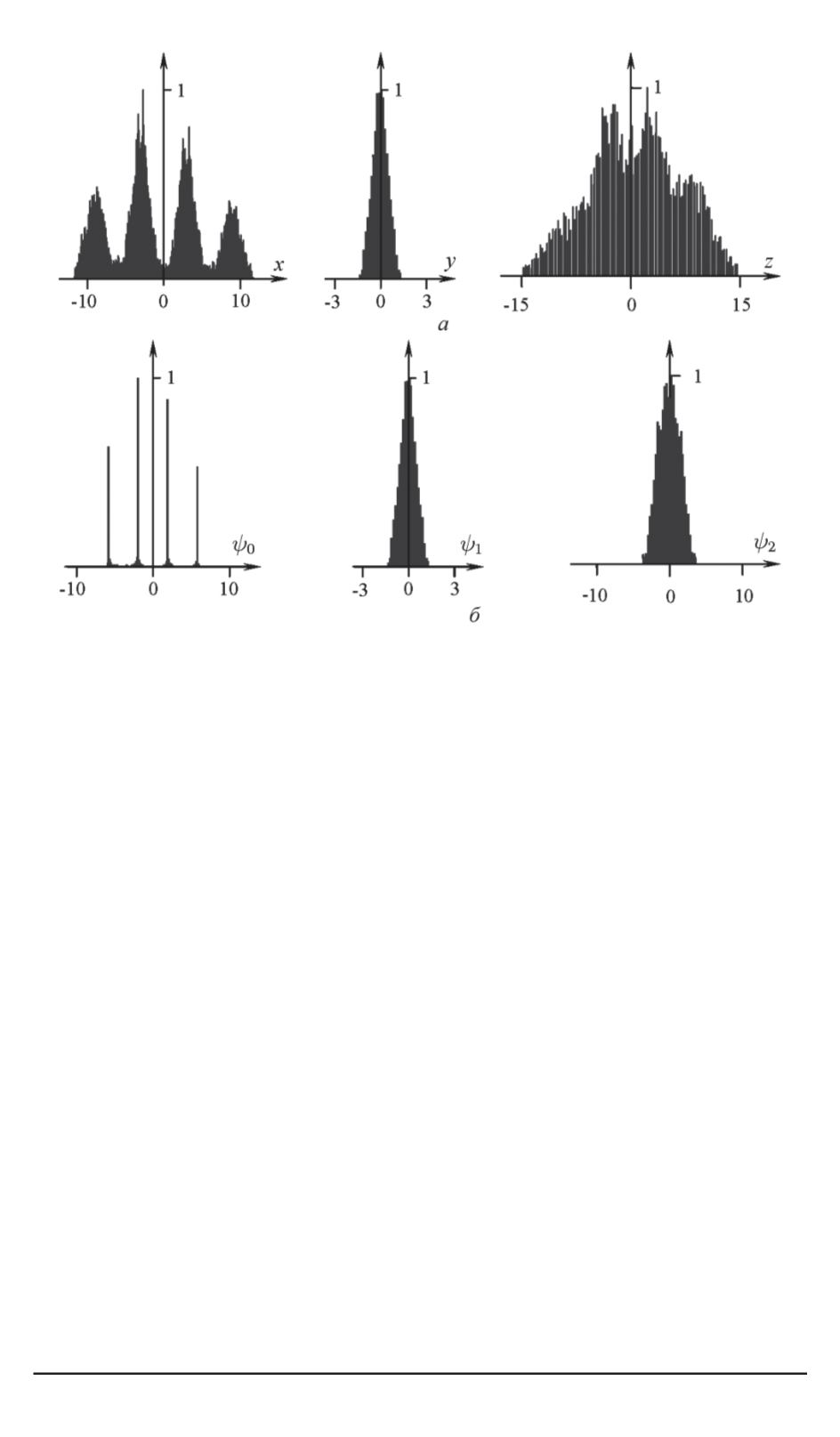
Рис. 6. Амплитудное распределение плотности значений независимых пере-
менных (
а
) и функций
ψ
0
, ψ
1
, ψ
2
(
б
) в системе (2). Обозначения и параметры
системы — см. рис. 2
С помощью преобразования (6) уравнения (2)–(4) могут быть за-
писаны относительно новых переменных
ψ
0
,
ψ
1
и
ψ
2
, что позволяет
свести изучение спектральных свойств колебаний в подобных систе-
мах к исследованию спектров функций
ψ
0
,
ψ
1
и
ψ
2
.
В этом случае одна изпеременных (
ψ
0
) будет в максимальной сте-
пени отражать общую (интегральную) структуру движения, включая
влияние числа сегментов в составе нелинейной функции, а остальные
(
ψ
1
и
ψ
2
) — его локальные особенности.
Это обусловлено тем, что первая описывает случайные переходы
фазовых траекторий между бассейнами притяжения положений равно-
весия, а остальные — движение внутри этих бассейнов в окрестности
положений равновесия. Вследствие этого в составе функции
ψ
0
под-
черкнута “медленная”, или импульсная, составляющая колебаний и
минимизирована быстроосциллирующая, или “быстрая”, составляю-
щая (см. рис. 5,
в
), а в составе функций
ψ
1
и
ψ
2
, наоборот, “медленная”
составляющая (см. рис. 5,
г, д
).
В результате отчетливую зависимость от числа сегментов пока-
зывает только спектр функции
ψ
0
, в то время как спектры функций
ψ
1
и
ψ
2
практически не изменяются при вариации числа сегментов
нелинейной функции.
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 1


