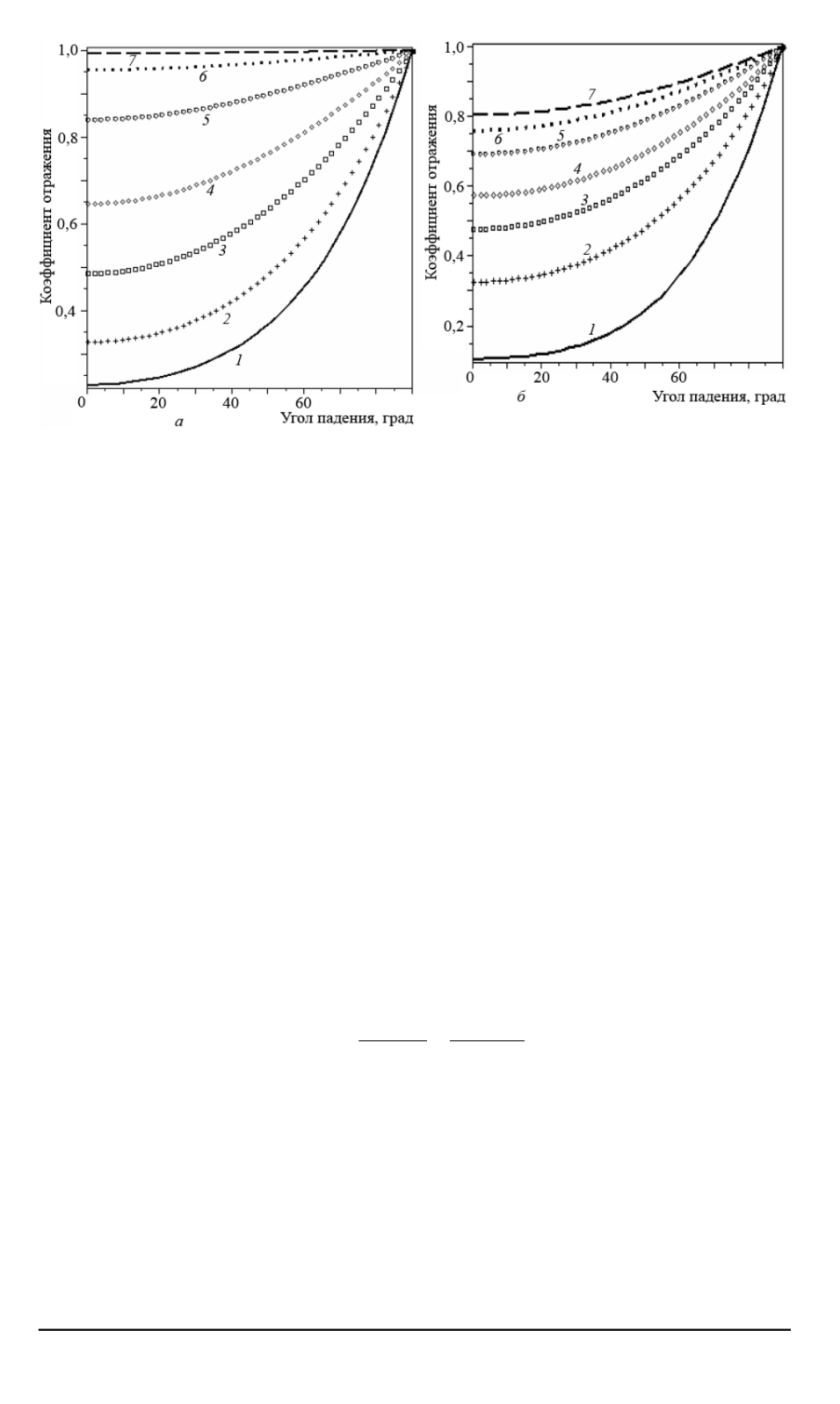
Рис. 3. Коэффициент отражения
S
-поляризованной волны в функции угла па-
дения:
а
—
n
= 2
,
α
= 0
; 1, 1,5, 2, 3, 5, 10 (соответственно кривые
1
,
2
,
3
,
4
,
5
,
6
,
7
);
б
—
α
= 1
,
n
= 1
, 2, 3, 4, 6, 8, 10 (соответственно кривые
1
,
2
,
3
,
4
,
5
,
6
,
7
)
электрического и магнитного полей (
~E
∙
~H
= 0
), которая является
следствием уравнения (5), ориентация вектора
~H
в плоскости падения
влечет за собой перпендикулярность плоскости падения вектору
~E
.
B рассматриваемом случае будем называть падающую электромаг-
нитную волну
P
-поляризованной, если справедливо соотношение
~H
k
=
H~e
y
.
(42)
Для действительных значений волнового вектора направление колеба-
ний вектора напряженности магнитного поля перпендикулярно плос-
кости падения в общепринятом понимании. Для вектора напряженно-
сти магнитного поля
~H
k
справедливы соотношения
i~k
∙
~H
k
= 0;
~ν
∙
~H
k
= 0;
~H
k
∙
~H
k
=
H
2
0
.
(43)
Вектор напряженности электрического поля определим из уравне-
ния (6) с учетом материальных уравнений среды
~E
k
=
1
−
iα
1 +
α
2
∙
~H
k
×
~k
ωεε
0
.
(44)
Следствием определения (44) являются соотношения
~E
k
∙
~k
= 0;
~E
k
∙
~H
k
= 0;
~E
k
∙
(
~k
×
~ν
) = 0
.
(45)
Таким образом, выполнены условия обобщенной поперечности элек-
тромагнитной волны, взаимной ортогональности электрического и
магнитного полей и условие
P
-поляризации электромагнитной волны.
Эти условия являются необходимыми для справедливости дисперси-
онного уравнения (8).
66
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 2


