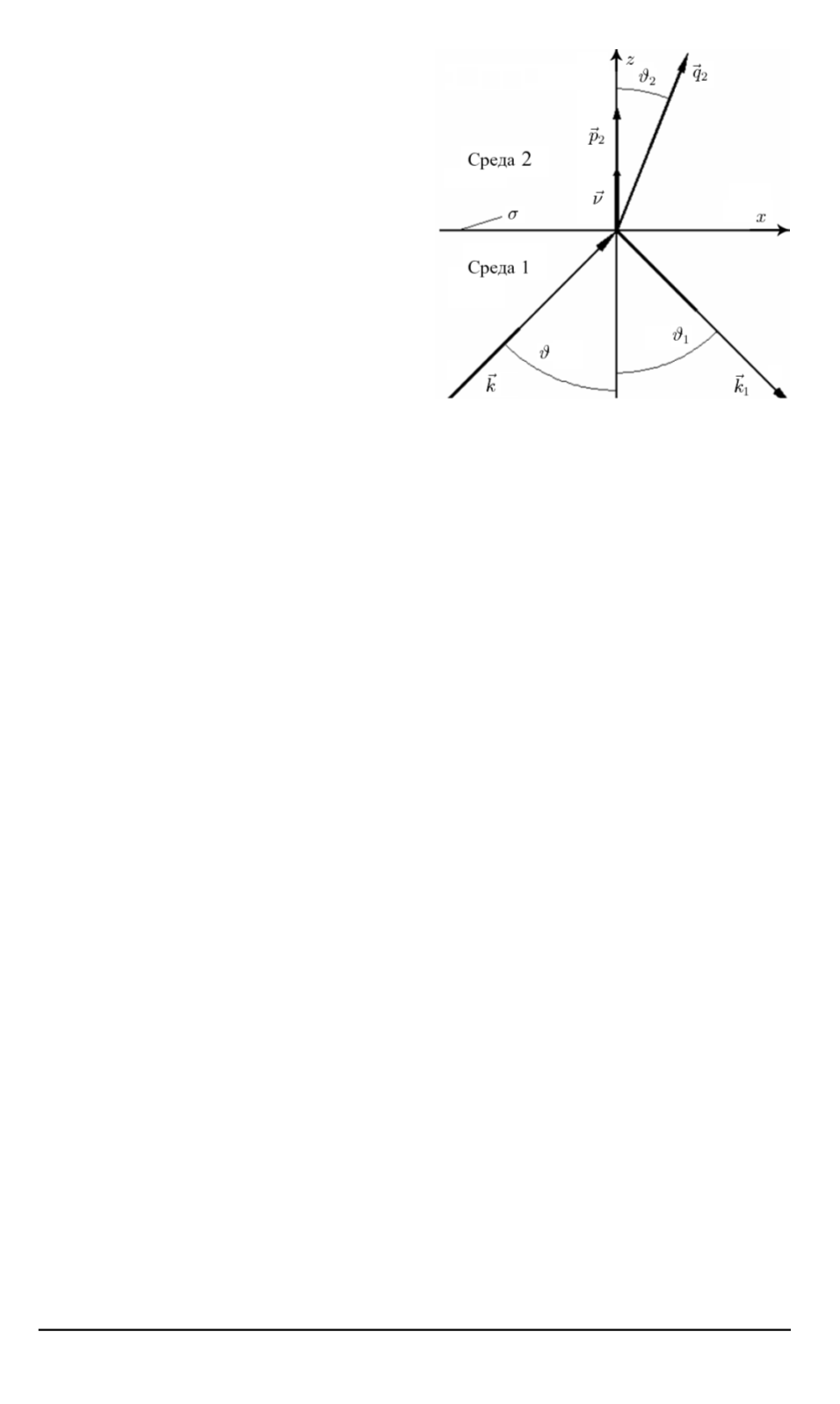
Рис. 1. Схема распространения излу-
чения при падении электромагнит-
ной волны на границу раздела двух
сред
Поместим начало декартовой
системы координат
{
x, y, z
}
на гра-
ницу раздела; положительное на-
правление оси
z
совпадает с на-
правлением нормали к границе раз-
дела; нижнее полупространство за-
полнено средой
1
, верхнее — сре-
дой
2
(рис. 1).
В развернутой форме соотно-
шения (20) с учетом условия одно-
родности падающей и отраженной
волн (
~p
= 0
,
~p
0
= 0)
имеют вид
q
x
=
q
0
x
;
q
y
=
q
0
y
;
q
x
=
q
00
x
;
p
00
x
= 0;
q
y
=
q
00
y
;
p
00
y
= 0
.
(21)
Кроме того, нормальные компонен-
ты волнового вектора падающей волны и волны, отраженной от по-
верхности раздела двух сред, связаны условием
q
z
=
−
q
0
z
.
(22)
Соотношение (22) справедливо, поскольку модули рассматриваемых
векторов одинаковы в силу распространения волн в одной и той же
среде (дисперсионные уравнения тождественны друг другу), а каса-
тельные компоненты одинаковы в силу условий (21).
Величины
q
00
z
и
p
00
z
подлежат определению с учетом дисперсион-
ного уравнения для второй (проводящей) среды и условий сопряже-
ния электромагнитного поля на границе раздела. Из системы условий
(21)–(22) следуют известные результаты: угол падения равен углу от-
ражения, волновые векторы падающей и отраженной волн лежат в
одной плоскости. Легко видеть, что действительная часть волнового
вектора преломленной волны лежит в той же плоскости, а его мнимая
часть перпендикулярна поверхности раздела (т.е. плоскость равных
амплитуд преломленной волны параллельна поверхности раздела). В
этих условиях всегда можно выбрать систему координат, в которой
плоскость падения электромагнитной волны совпадает с плоскостью
y
= 0
, при этом, естественно, выполняется условие
q
y
= 0
. След-
ствием условий (21) является также обобщенный закон преломления
Снеллиуса
q
sin
ϑ
=
q
00
sin
ϑ
00
(23)
с той лишь разницей, что величина
q
00
должна рассматриваться как
функция угла преломления
ϑ
00
(угол
ψ
в рассматриваемом случае со-
впадает с углом преломления
ϑ
00
)
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 2
61


