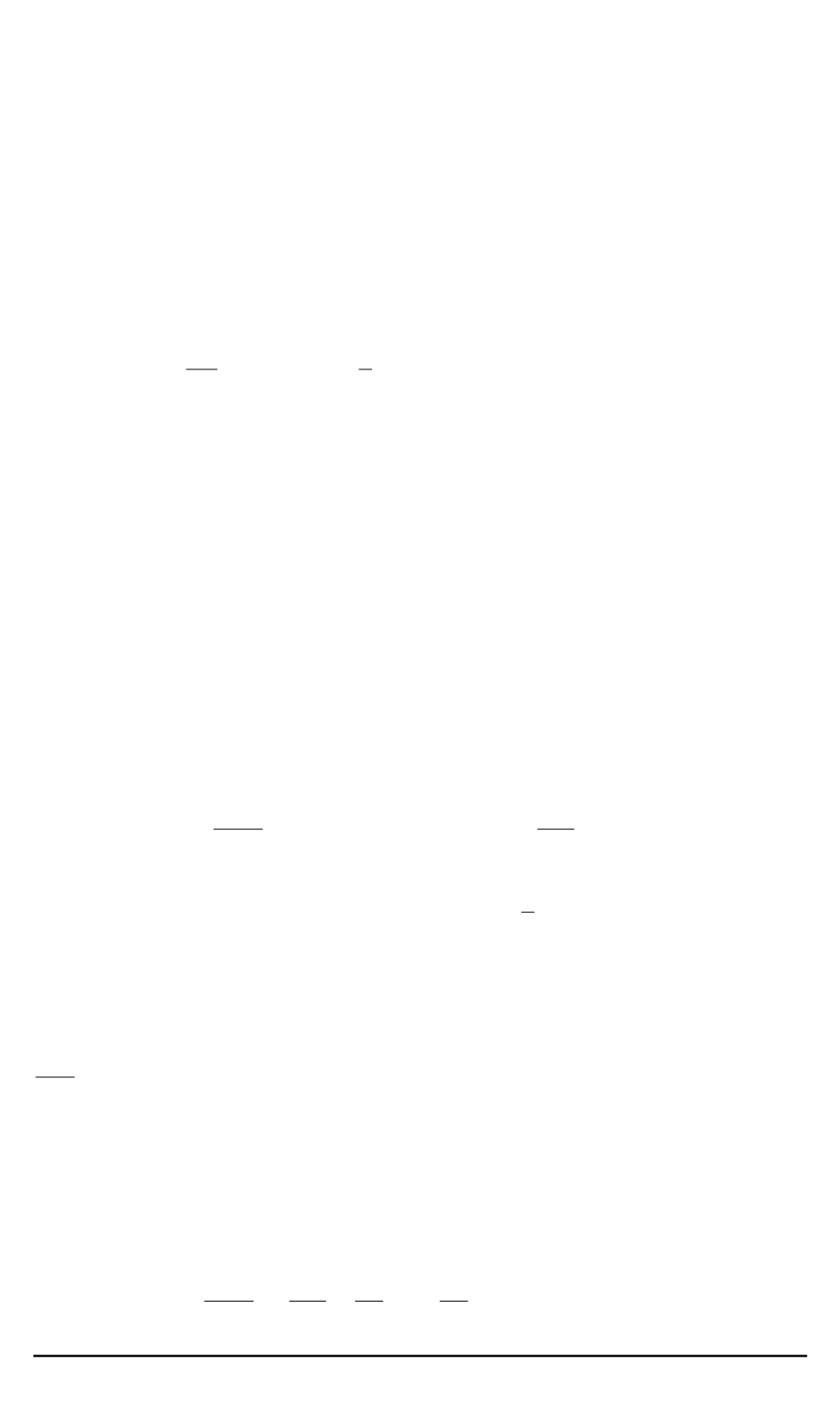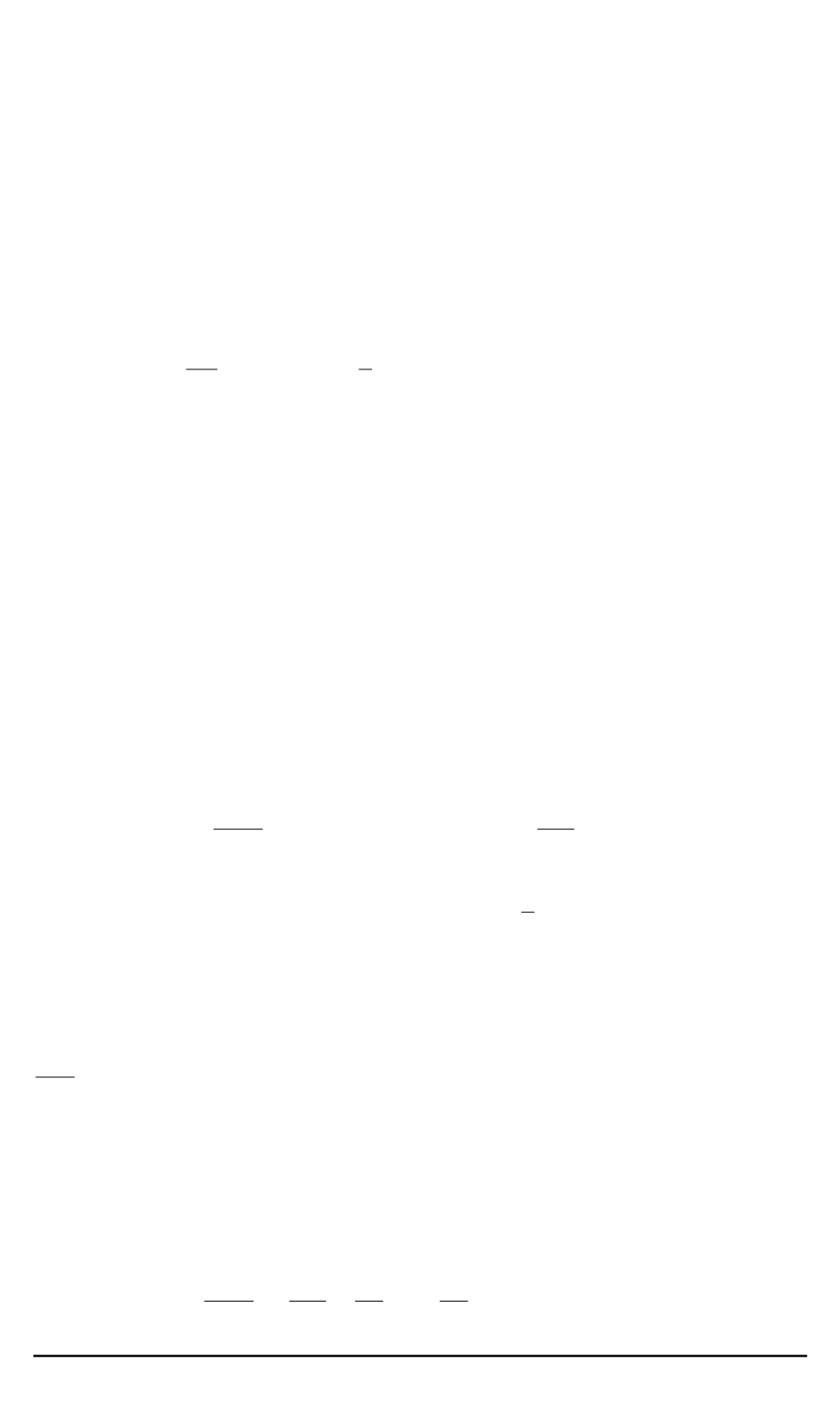
т.е.
ρE
=
N
X
α
=1
ρ
α
E
α
=
Z
V
N
X
α
=1
ρ
α
u
α
+
k
α
dV,
где
ρ
α
E
α
— объемная плотность полной энергии
α
-го компонента сме-
си;
u
α
— массовая плотность внутренней энергии
α
-го компонента
смеси;
k
α
=
ρ
α
α
v
i
α
v
i
/
2
— объемная плотность кинетической энергии
α
-
го компонента в рассматриваемой материальной макроточке. Для
α
-го
компонента смеси закон сохранения энергии имеет вид
α
D
Dt
Z
V
ρ
α
u
α
+
1
2
ρ
α
α
v
i
α
v
i
dV
=
Z
S
α
p
i
α
v
i
dS
+
+
Z
V
α
b
i
α
v
i
dV
+
Z
V
α
q
V
dV
−
Z
S
α
q
i
n
i
dS
+
Z
V
N
X
ν
=1
E
να
dV,
(11)
где
α
q
V
— объемная плотность мощности внутренних источников (или
стоков) теплоты в
α
-м компоненте смеси;
α
q
i
— составляющие вектора
плотности теплового потока
q
i
=
N
X
α
=1
α
q
i
;
E
να
определяет интенсивность
энергообмена между
α
-м и
ν
-м компонентами смеси,
E
να
=
−
E
αν
,
E
αα
= 0
.
Локальная формулировка закона сохранения энергии очевидна:
ρ
α
α
Du
α
Dt
=
α
σ
(
ji
)
α
V
ij
+
α
σ
<ji>
α
W
ij
−
∂
α
q
i
∂x
i
+
α
q
V
+
+
N
X
ν
=1
E
να
−
να
P
i
α
v
i
−
J
να
u
α
−
1
2
α
v
i
α
v
i
= 0
,
(12)
где
α
σ
(
ji
)
,
α
σ
<ji>
— компоненты симметричной и антисимметричной
частей тензора напряжений
α
-го компонента,
α
σ
ji
=
α
σ
(
ji
)
+
α
σ
<ji>
;
∂
α
v
i
∂x
j
=
α
V
ij
+
α
W
ij
;
α
V
ij
= (
∂
α
v
i
/∂x
j
+
∂
α
v
j
/∂x
i
)
/
2
— компоненты тен-
зора скоростей;
α
W
ij
= (
∂
α
v
i
/∂x
j
−
∂
α
v
j
/∂x
i
)
— компоненты тензора
завихренности.
Второй закон термодинамики в виде неравенства Клаузиуса–
Дюгема для
α
-го компонента смеси можно записать в виде
ρ
α
α
Dh
α
Dt
+
∂
∂x
i
α
q
i
T
α
!
−
α
q
V
T
α
−
ρ
α
N
X
ν
=1
h
να
>
0
,
40
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 3