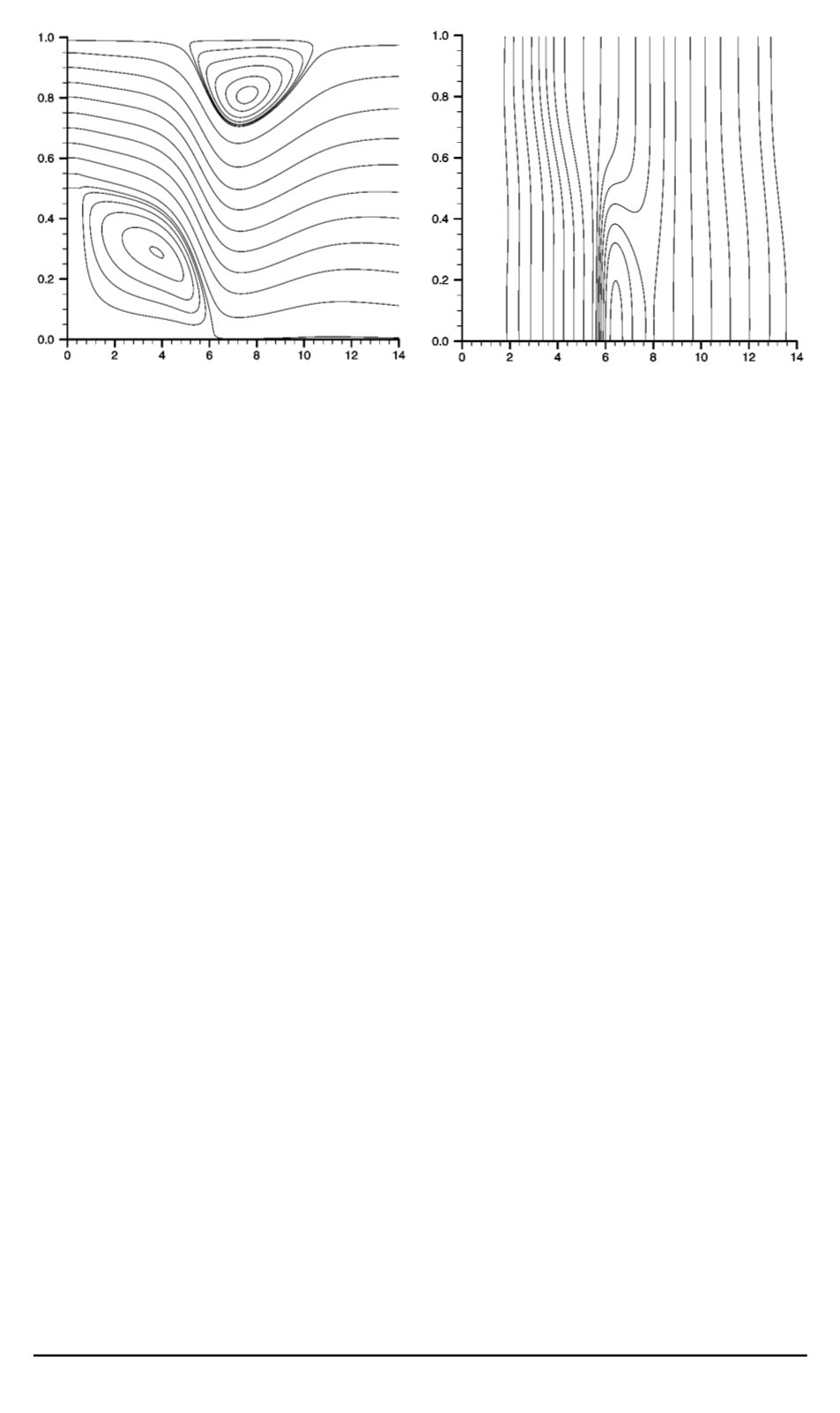
Рис. 8. Изолинии функции тока при об-
текании ступеньки (
Re = 800
)
Рис. 9. Изобары функции тока при об-
текании ступеньки (
Re
= 800
)
показаны изобары. Очевидно, что, за исключением небольшой под-
области, изобары — почти вертикальные линии, т.е. давление в данной
задаче изменяется преимущественно в направлении потока. Поэтому
”градиент давления”
(
p
x
)
0
x
, отыскиваемый при помощи вспомогатель-
ной задачи, будет доминирующим. Преобладание
(
p
x
)
0
x
приводит к
существенному снижению трудоемкости вычислений для отыскания
слагаемого
p
xy
в (11). Заметим, что при увеличении отношения
L/H
будет наблюдаться дальнейший рост эффективности МСА по сравне-
нию с КСА.
Выводы.
Предложенный алгоритм для решения уравнений Навье–
Стокса в переменных скорость–давление на структурированных сет-
ках занимает промежуточное место между сегрегированными и со-
вместными алгоритмами, поскольку компоненты скорости и “часть
давления”
p
x
+
p
y
всегда отыскиваются совместно при решении вспо-
могательной задачи.
Организация вычислений по схеме предиктор–корректор, где в ка-
честве предиктора используется вспомогательная задача, позволяет
уменьшить объем вычислений, необходимых для решения уравнений
Навье–Стокса в переменных скорость–давление на структурирован-
ных сетках. Уменьшение трудоемкости вычислений особенно заметно
при моделировании течений с выделенным направлением течения сре-
ды.
Решение вспомогательной задачи не требует глобальной линеари-
зации матрицы коэффициентов результирующей системы алгебраиче-
ских уравнений. Поэтому данный метод может быть легко обобщен
для моделирования течений сжимаемых сред, теплофизические свой-
ства которых далеки от свойств совершенного газа.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
93


