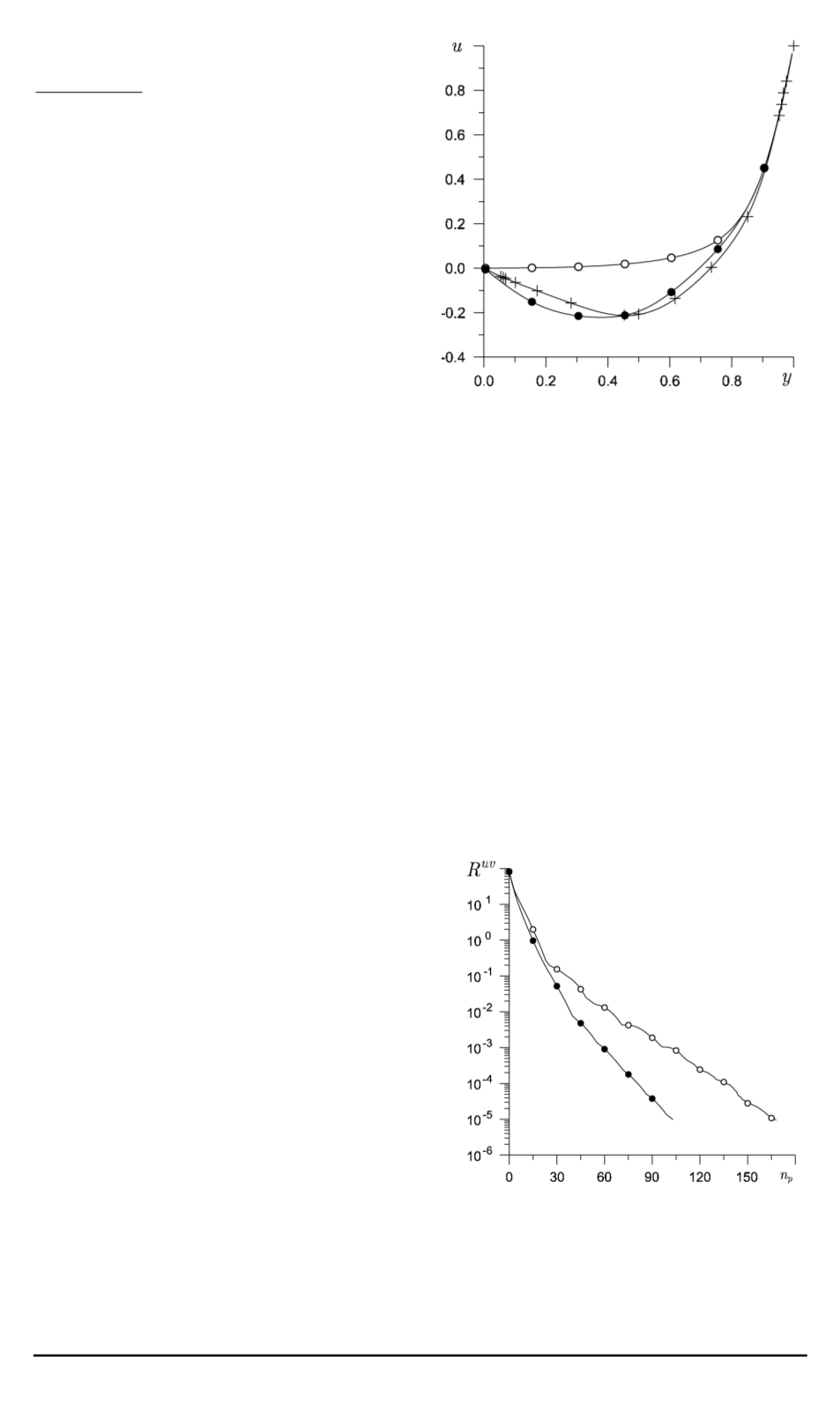
Рис. 2. Распределение компоненты
скорости
u
(0
,
5
, y
)
в вертикальном се-
чении, проходящeм через середину
дна каверны, при
Re = 100
:
+
данные работы [7]; —— — расчет;
◦
—
КСА;
•
— МСА
останова итераций задан в виде
k
Ax
−
b
k
k
b
k
<
10
−
7
.
Расчет течения
при
Re = 100
проводился на равно-
мерной разнесенной сетке
101
×
101
(
h
x
=
h
y
= 1
/
100
).
На рис. 2 проиллюстрирова-
ны преимущества использования
уравнений постоянства массового
расхода (9) и (10) в качестве апри-
орной информации. На рисунке
сплошной линией показано полу-
ченное решение уравнений Навье–
Стокса в переменных скорость–
давление, а маркерами “+” — в пе-
ременных вихрь–функция тока [7].
Начальное приближение в КСА,
полученное из (23), близко к ре-
шению только в непосредственной близости от движущейся крышки
(
y >
0
,
7
). Начальное приближение в МСА, полученное из (24), близко
к решению во всем вертикальном сечении.
Естественно ожидать, что скорость сходимости МСА будет выше,
чем КСА. На рис. 3 показано уменьшение погрешности уравнения не-
разрывности
R
uv
(22) в процессе выполнения итераций по давлению
(
n
p
). Использование вспомогательной задачи (12) и (13) в МСА при-
вело к уменьшению числа итераций по давлению приблизительно в
полтора раза.
Рис. 3. Зависимость погрешности
разностного аналога уравнения не-
разрывности
R
uv
от числа итера-
ций по давлению
n
p
:
◦
— КСА;
•
— МСА
Следующий этап тестирования
МСА — расчет течения в каверне при
Re = 1000
. В этом случае итера-
ции по нелинейности будут расхо-
диться при нулевом начальном при-
ближении, поэтому необходимо при-
нять дополнительные меры для обес-
печения сходимости. Принят наибо-
лее распространенный способ полу-
чения стационарного решения по-
добных задач путем счета на устано-
вление. Этим же показана примени-
мость МСА к решению нестационар-
ных уравнений Навье–Стокса. Рас-
чет течения при
Re = 1000
проводи-
ли на равномерной сетке
301
×
301
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
89


