L
Z
−
H/
2
v
(
x, y
)
dx
=
−
y
Z
0
u
(
L, ξ
)
dξ
+
y
Z
H/
2
u
(
−
H/
2
, ξ
)
dξ
при
H/
2
< y
6
H.
Для удобства доопределим компоненты скорости, полагая их рав-
ными нулю в ступеньке, т.е.
u
(
x, y
) =
v
(
x, y
) = 0
при
−
H/
2
6
x
6
0
и
0
6
y
6
H/
2
.
Тогда уравнения постоянства массового расхода упрощаются и при-
нимают вид
H
Z
0
u
(0
, y
)
dy
=
H
Z
0
u
(
x, y
)
dy
;
L
Z
0
v
(
x, y
)
dx
=
−
y
Z
0
u
(
L, ξ
)
−
u
(0
, ξ
)
dy.
В качестве примера выполнен расчет обтекания ступеньки при
Re = 800
,
L
= 14
H
. Расчет проводился на равномерной разнесен-
ной сетке
101
×
1401
(
h
x
=
h
y
= 1
/
100
). Получено, что при более
высоких значениях числа Рейнольдса уже не существует стационар-
ного течения.
Изолинии функции тока показаны на рис. 8, а в таблице приводит-
ся сопоставление полученных результатов
1
с ранее опубликованными
данными.
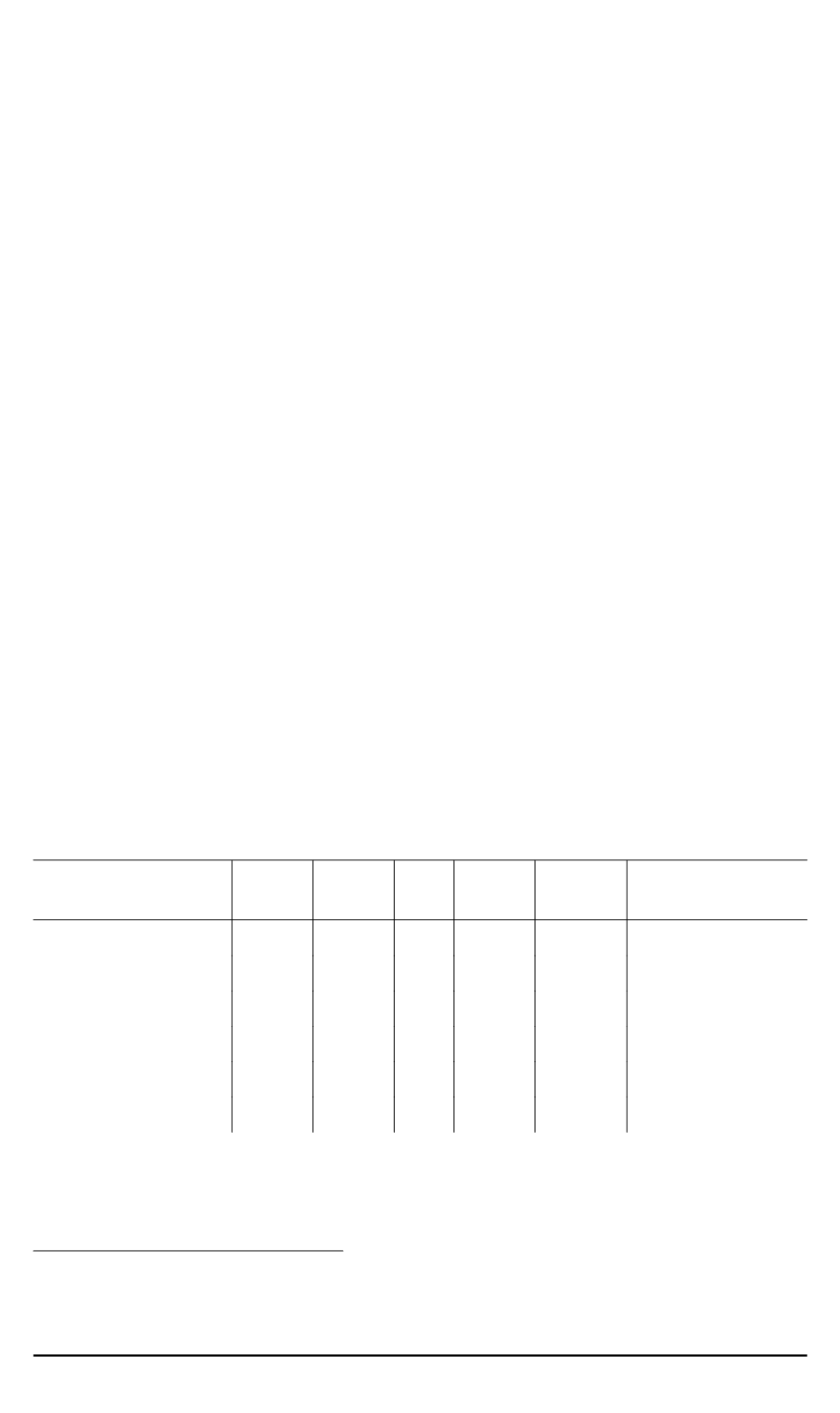
Таблица
Сравнение результатов моделирования течения при обтекании ступеньки
(
Re
= 800
)
Литературный
источник
l
B
l
T
w
T
x
TL
x
TR
Число узлов
[8]
6,0150 5,6600 – 4,8200 10,4800
[9]
6,1000 5,6300 – 4,8500 10,4800 129681
[10]
6,0820 5,6260 – 4,8388 10,4648 245760
[10]
6,1000 5,6300 – 4,8600 10,4900
>
8000
[11]
6,0964 5,6251 – 4,8534 10,4785 3737
Данная работа 6,1000 5,6300 0,28 4,8400 10,4700 141501
Сравнение времени решения задачи об обтекании ступеньки пока-
зывает, что объем вычислений в МСА при
L/H
= 14
приблизительно
в 300 раз меньше, чем в КСА. Причина этого понятна из рис. 9, где
1
В настоящей работе границей вихрей считались узлы, в которых сеточная функ-
ция
u
ij
меняет знак, т.е. координаты точек отрыва и присоединения
x
TL
,
x
TR
и
l
B
определялись с точностью до шага сетки
h
x
= 1
/
100
.
92
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


