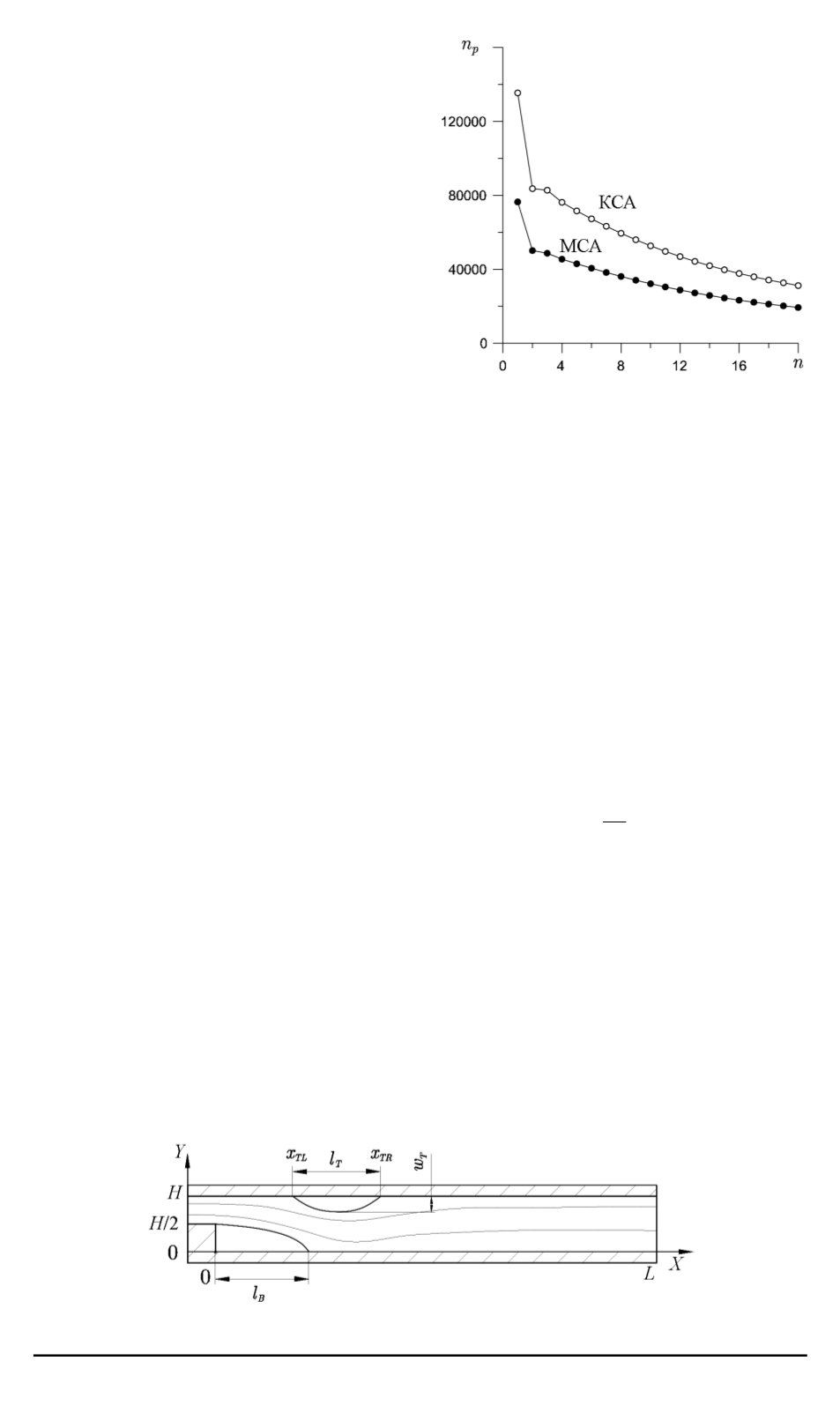
Рис. 6. Зависимость числа выполнен-
ных итераций
n
p
по давлению, не-
обходимых для достижения крите-
рия останова, от числа
n
временных
слоев
Поскольку в основе вспомога-
тельной задачи лежат упрощения,
характерные для урaвнений Навье–
Стокса в приближении погранич-
ного слоя или длинного канала,
то уменьшение объема вычислений
в МСА по сравнению с КСА на
примере расчета течения в кавер-
не является минимальным.
Задача об обтекании ступень-
ки при
Re = 800
часто применяет-
ся для тестирования вычислитель-
ных алгоритмов решения уравне-
ний Навье–Стокса. Расчетная схе-
ма задачи показана на рис. 7. Рас-
сматривается стационарное тече-
ние среды с постоянными свойствами в канале длиной
L
и высотой
H
. На входе в канал расположена ступенька размера
H/
2
×
H/
2
. Пред-
полагается, что на входе в канал компонента скорости
u
распределена
по параболическому закону, а
v
= 0
. При больших числах Рейнольдса
образуются два вихря — непосредственно за ступенькой и на верхней
стенке канала.
Запишем интегральные формы уравнения неразрывности для дан-
ной задачи:
H
Z
H/
2
u
(
x, y
)
dy
=
H
Z
H/
2
u
(
−
H/
2
, y
)
dy
при
−
H
2
6
x
6
0;
H
Z
0
u
(
x, y
)
dy
=
H
Z
H
/
2
u
(
−
H/
2
, y
)
dy
при
0
< x
6
L
;
L
Z
0
v
(
x, y
)
dx
=
−
y
Z
0
u
(
L, ξ
)
dξ
при
0
6
y
6
H/
2;
Рис. 7. Расчетная схема задачи об обтекании ступеньки
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
91


