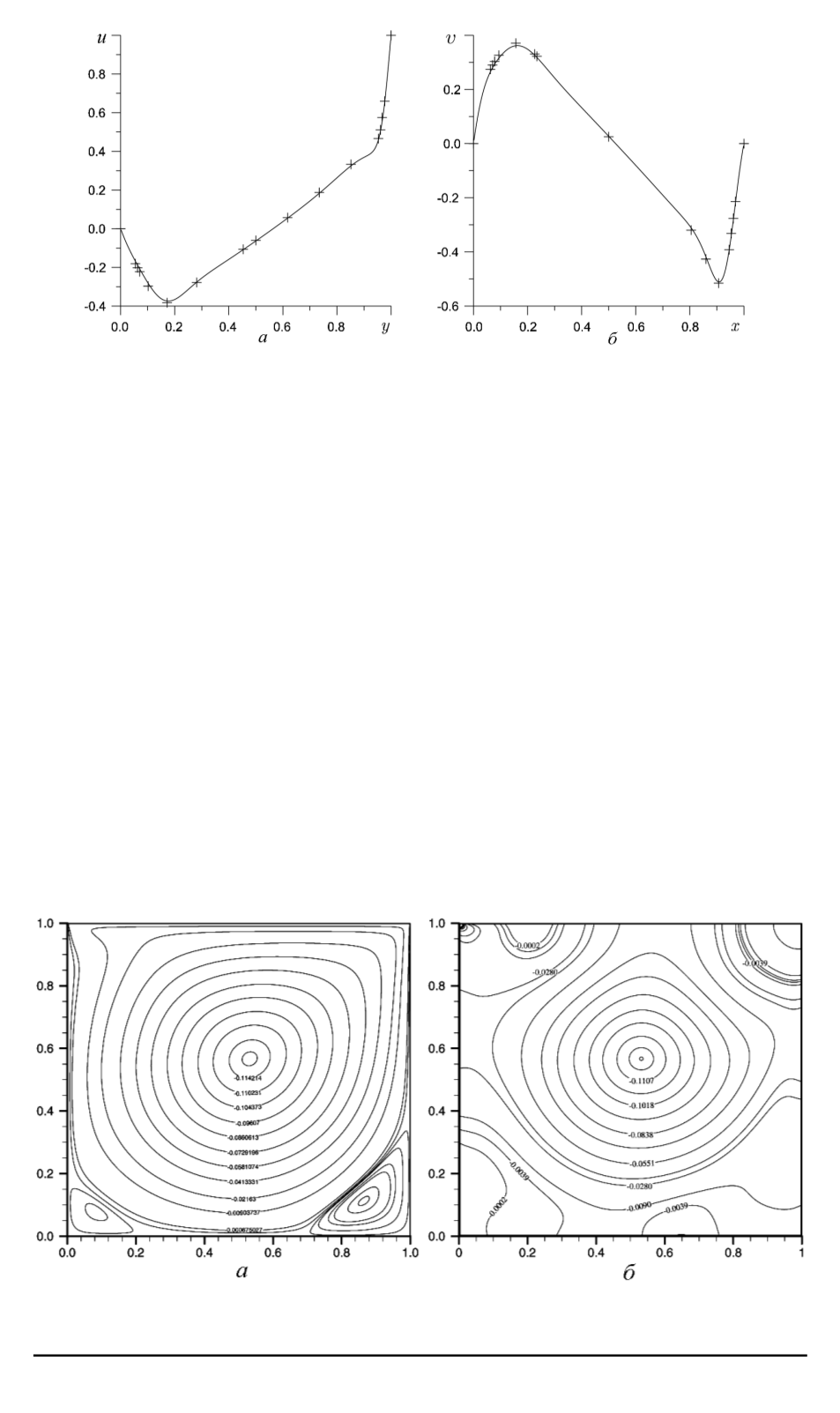
Рис. 4. Распределение компоненты скорости
u
в вертикальном сечении, прохо-
дящем через середину дна каверны (
a
), и распределение компоненты скорости
v
в горизонтальном сечении, проходящем через середину боковых стенок ка-
верны (
б
), при
Re = 1000
(+ — данные работы [7])
На рис. 4 сопоставлены компоненты скорости
u
и
v
в характерных
сечениях каверны с результатами решений уравнений Навье–Стокса в
переменных вихрь–функция тока [7]. Изолинии функции тока и изо-
бары показаны на рис. 5.
Число выполненных итераций по давлению (
n
p
), необходимое для
достижения критерия останова (22) на первых двадцати временных
слоях
n
, показано на рис. 6. В МСА одна
P
-итерация выполнялась
после каждой сотой итерации по давлению, поэтому вычислительная
стоимость каждой итерации по давлению в МСА и КСА практиче-
ски одинакова. Как и при решении стационарных уравнений Навье–
Стокса, вспомогательная задача позволила сократить объем вычисле-
ний приблизительно в полтора раза.
Рис. 5. Изолинии (
а
) функции тока (
Re
= 1000
) и изобары (
б
) (
Re
= 1000
,
p
(0
,
0) = 0
) при течении в каверне
90
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2


