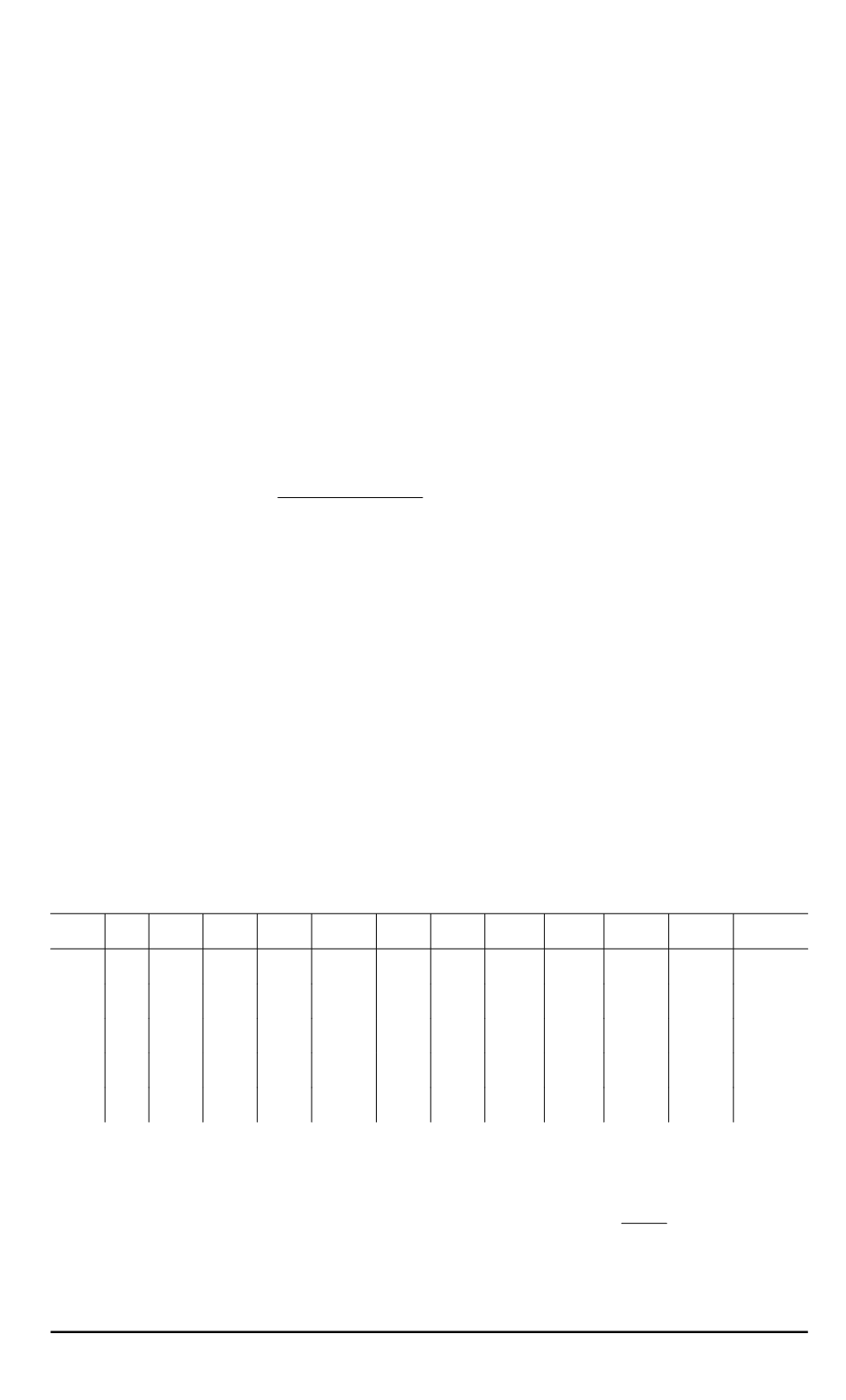
только в том случае, если
λ
2
≤
λ
1
≤
λ
3
(λ
3
≤
λ
1
≤
λ
2
)
, т.е.
2
p
−
4
−
L
−
9
|
M
| ≤
2
p
−
16 + 2
L
≤
2
p
−
4
−
L
+ 9
|
M
|
. После
преобразования получаем неравенство
−
3
|
M
| ≤
L
−
4
≤
3
|
M
|
, рав-
носильное неравенству
|
L
−
4
| ≤
3
|
M
|
.
Таким образом, лемма 2.1 определяет достаточные условия суще-
ствования квазиодноуровневых РМ с
1
S
≤
1
S
max
. Если
1
S
max
— за-
данное пороговое значение, то РМ будет квазиодноуровневым при зна-
чениях
p
, удовлетворяющих условиям
|
L
−
4
| ≤
3
|
M
|
,
|
M
| ≤
1
S
max
.
Лемма 2.1 определяет значения
p
, при которых
1
S
достигает наи-
меньшего значения при фиксированном
M
. Найдем значения
p
, при
которых число уровней РМ минимально.
Теорема 2.1.
Если
d
=
3
, то множество степенных вычетов
H
k
является РМ, сбалансированным на два уровня, в том и только в том
случае, если
p
=
36
u
2
−
24
u
+ 7
, где
u
— целое число; при этом
1
S
= |
2
u
−
1
|
,
γ
= |
2
u
−
1
|
12
u
2
−
8
u
+ 2
. В остальных случаях РМ сбалан-
сировано на три уровня.
Доказательство
. РМ будет сбалансировано на два уровня, если
λ
1
=
λ
2
или
λ
1
=
λ
3
. Таким образом, должно выполняться равенство
2
p
−
16+2
L
=
2
p
−
4
−
L
±
9
M
или
±
3
M
=
L
−
4
. Тогда
p
=
L
2
−
6
L
+
+
12
, а так как
p
— простое число, то
L
— нечетно. Следовательно,
L
=
1+6
u
и
p
=
36
u
2
−
24
u
+7
(
4
p
=
(
1+6
u
)
2
+27
(
2
u
−
1
)
2
)
. Подставляя
L
=
1 + 6
u
и
M
=
2
u
−
1
в (1) получаем, что
λ
1
=
λ
3
=
4
u
2
−
2
u
,
λ
2
=
4
u
2
−
4
u
+ 1
.
В качестве примера в табл. 1 приведены параметры РМ, удовлетво-
ряющих условиям теоремы 2.1.
Таблица 1
Параметры РМ, сбалансированных на два уровня, для
p
=
3
R
+ 1
u
0 1 – 1 2 – 2 4 5 – 6 – 8 9 – 10 11
p
7 19 67 103 199 487 787 1447 2503 2707 3847 4099
R
2 6 22 34 66 162 262 482 834 902 1282 1366
λ
min
0 1 6 9 20 49 81 159 272 289 420 441
1
S
1 1 3 3 5 7 9 10 17 17 21 21
γ
0,5 0,16 0,13 0,08 0,075 0,04 0,03 0,02 0,02 0,018 0,016 0,015
Как следует из таблицы, значения
γ
быстро убывают с возраста-
нием
|
u
|
, в частности справедливо неравенство
γ
≤
1
5
|
u
|
для
u
6
=
0
.
Теорема 2.1 определяет достаточные условия существования двух-
уровневых РМ при
d
=
3
. Если
1
S
max
— заданное пороговое значение,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4
11


