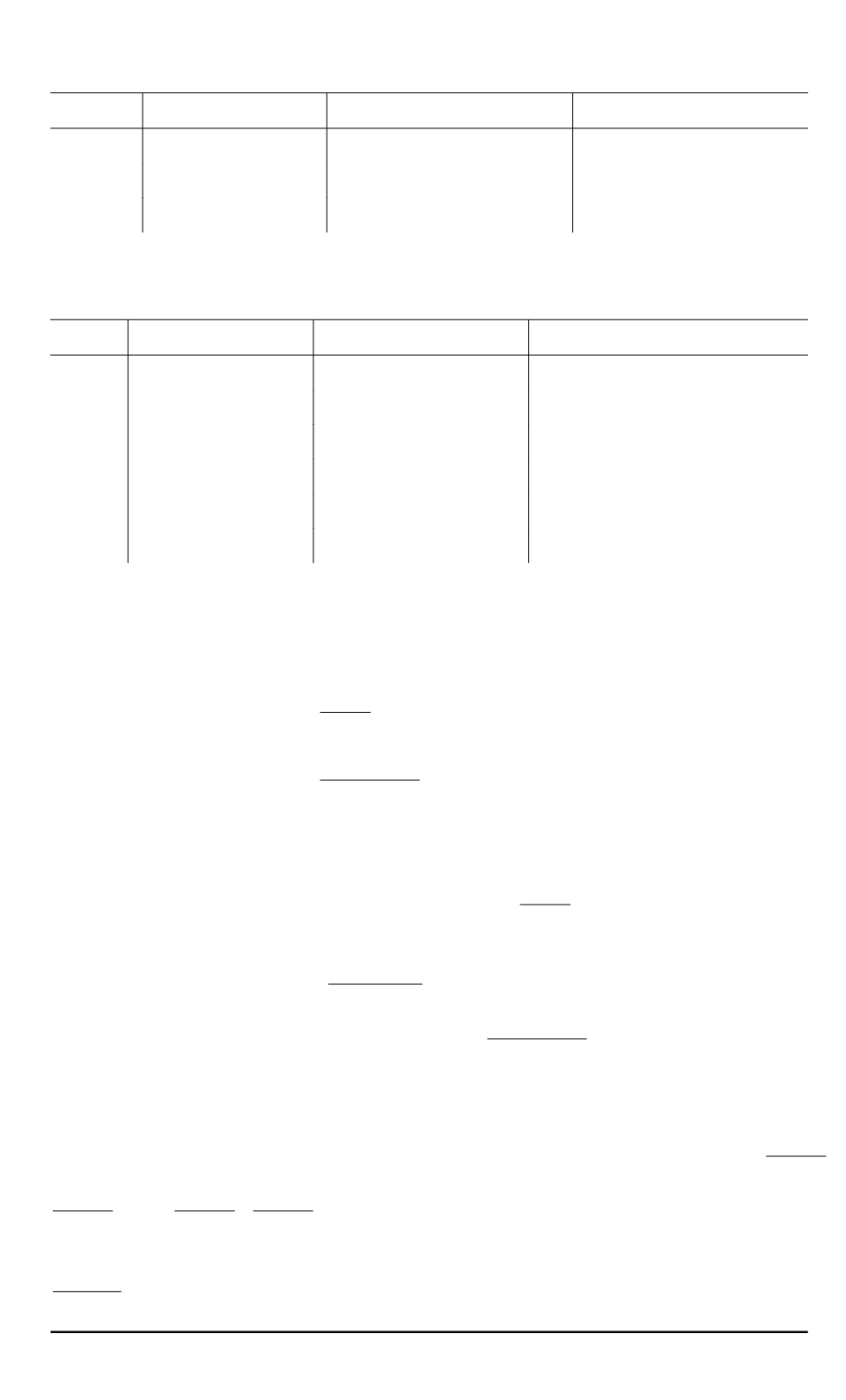
Таблица 2
Гармоники СРКВ для
p
=
6
R
+ 1
при нечетном
R
m
=
0
m
=
1
m
=
2
36
λ
1
9
p
−
27 + 24
B
9
p
−
27
9
p
−
27
−
12
A
+ 12
B
36
λ
2
9
p
−
27
9
p
−
27 + 12
A
+ 12
B
9
p
−
27 + 12
A
−
12
B
36
λ
3
9
p
−
27
−
24
B
9
p
−
27
−
12
A
−
12
B
9
p
−
27
Таблица 3
Гармоники СРКВ для
p
=
6
R
+ 1
при четном
R
m
=
0
m
=
1
m
=
2
36
λ
1
9
p
−
45 + 24
B
9
p
−
45
9
p
−
45
−
12
A
+ 12
B
36
λ
2
9
p
−
45
9
p
−
45 + 12
A
+ 12
B
9
p
−
45 + 12
A
−
12
B
36
λ
3
9
p
−
45
−
24
B
9
p
−
45
−
12
A
−
12
B
9
p
−
45
36
λ
4
9
p
−
9 + 24
B
9
p
−
9
9
p
−
9
−
12
A
+ 12
B
36
λ
5
9
p
−
9
9
p
−
9 + 12
A
+ 12
B
9
p
−
9 + 12
A
−
12
B
36
λ
6
9
p
−
9
−
24
B
9
p
−
9
−
12
A
−
12
B
9
p
−
9
Теорема 4.1.
Если
{
k
,
l
,
n
} 2
J
и
R
— нечетное, то для РМ
G
максимальная разница между уровнями
1
S
=
4
|
B
|
3
при
B
≡
0
(
mod3
)
,
2
|
A
±
B
|
3
при
B
6
≡
0
(
mod3
).
Доказательство
. Если
m
=
0
, то согласно первому столбцу
табл. 2
λ
3
≤
λ
2
≤
λ
1
при
B
>
0
и
λ
1
≤
λ
2
≤
λ
3
при
B
<
0
. Та-
ким образом,
1
S
= |
λ
3
−
λ
1
|
или
1
S
=
4
|
B
|
3
. Если же
m
=
1
, то
λ
3
≤
λ
1
≤
λ
2
при
A
+
B
>
0
и
λ
2
≤
λ
1
≤
λ
3
при
A
+
B
<
0
,
тогда
1
S
= |
λ
3
−
λ
2
| =
2
|
A
+
B
|
3
согласно второму столбцу табл. 2.
Аналогично при
m
=
2
величина
1
S
=
2
|
A
−
B
|
3
.
Следствие 4.1.
Если
p
=
4
(
3
u
−
1
)
2
+3
(
1 + 6
u
)
2
или
p
=
4
(
2 + 3
u
)
2
+
+
3
(
1 + 6
u
)
2
, то множество степенных вычетов
H
k
∪
H
l
∪
H
n
при
{
k
,
l
,
n
} 2
J
является РМ, сбалансированным на три уровня,
D p
,
p
−
1
2
,
p
−
3
4
−
1
,
p
−
3
4
,
p
−
3
4
+ 1
с
1
S
=
2
.
Доказательство.
Для значений
p
, определяемых следствием 4.1,
A
±
B
3
= ±
1
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4
15


