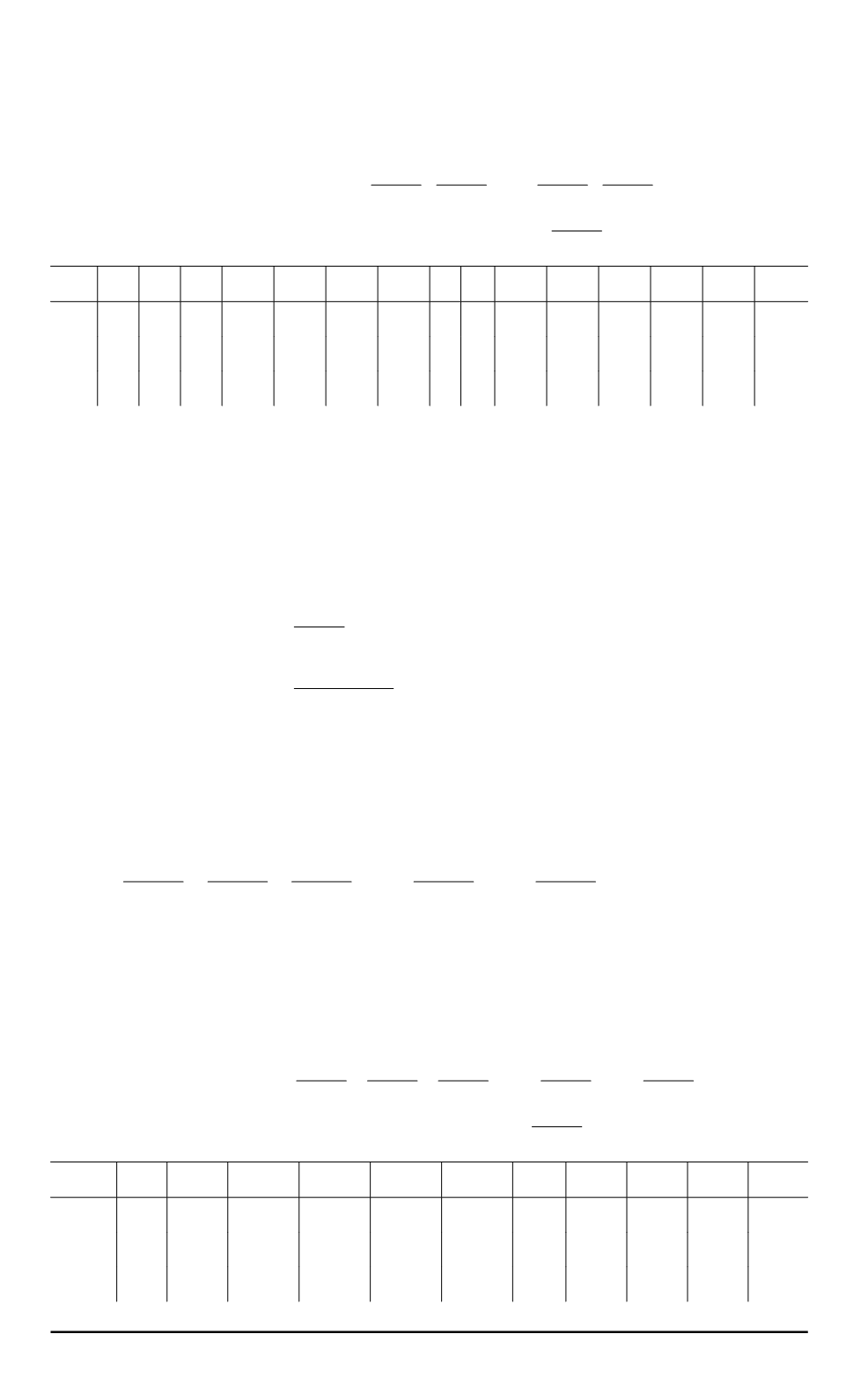
В качестве примера в табл. 4 приведены параметры РМ для значе-
ний
p
, определяемых следствием 4.1.
Таблица 4
Параметры РМ
D p
,
p
−
1
2
,
p
−
3
4
−
1
,
p
−
3
4
,
p
−
3
4
+ 1
для
p
=
6
R
+ 1
с
1
S
=
2
и
γ
=
4
p
−
1
u
– 1 1 2 – 5 – 6 – 8 8 0 – 1 – 3 3 – 4 4 – 8 8
p
139 163 607 3547 5119 9127 9319 19 79 1063 1567 1987 2659 8563 9907
3
R
69 81 303 1773 2559 4563 4659 9 39 531 783 993 1329 4281 4953
λ
min
33 39 150 885 1278 2280 2328 3 18 264 390 495 663 2139 2475
Исследуем теперь случай четного
R
. (В работе [3] ошибочно пола-
гают, что здесь возможны два уровня.)
Теорема 4.2.
Если
{
k
,
l
,
n
} 2
J
и
R
— четное, то для РМ
G
макси-
мальная разница между уровнями
1
S
=
4
|
B
|
3
+ 1
при
B
≡
0
(
mod3
)
,
2
|
A
±
B
|
3
+ 1
при
B
6
≡
0
(
mod3
).
Доказательство теоремы 4.2 следует из анализа табл. 3.
Следствие 4.2.
Если
p
=
144
u
2
−
60
u
+ 13
или
p
=
144
u
2
+
+
156
u
+ 49
, то множество степенных вычетов
H
k
∪
H
l
∪
H
n
при
{
k
,
l
,
n
} 2
J
является РМ, сбалансированным на четыре уровня,
D p
,
p
−
1
2
,
p
−
9
4
,
p
−
9
4
+ 1
,
p
−
9
4
+ 2
,
p
−
9
4
+ 3
с
1
S
=
3
.
В качестве примера в табл. 5 приведены параметры РМ, сбалан-
сированных на четыре уровня, для значений
p
, определяемых след-
ствием 4.2.
Таблица 5
Параметры РМ
D p
,
p
−
1
2
,
p
−
9
4
,
p
−
9
4
+ 1
,
p
−
9
4
+ 2
,
p
−
9
4
+ 3
для
p
=
6
R
+ 1
с
1
S
=
3
и
γ
=
6
p
−
1
u
1 – 2 3
– 4
5
– 6 – 1 – 2 1 – 3 2
p
97 709 1129 2557 3313 5557 37 313 349 877 937
3
R
48 354 564 1278 1656 2778 18 156 174 438 468
λ
min
22 175 280 637 826 1387 7 76 85 217 232
16
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


