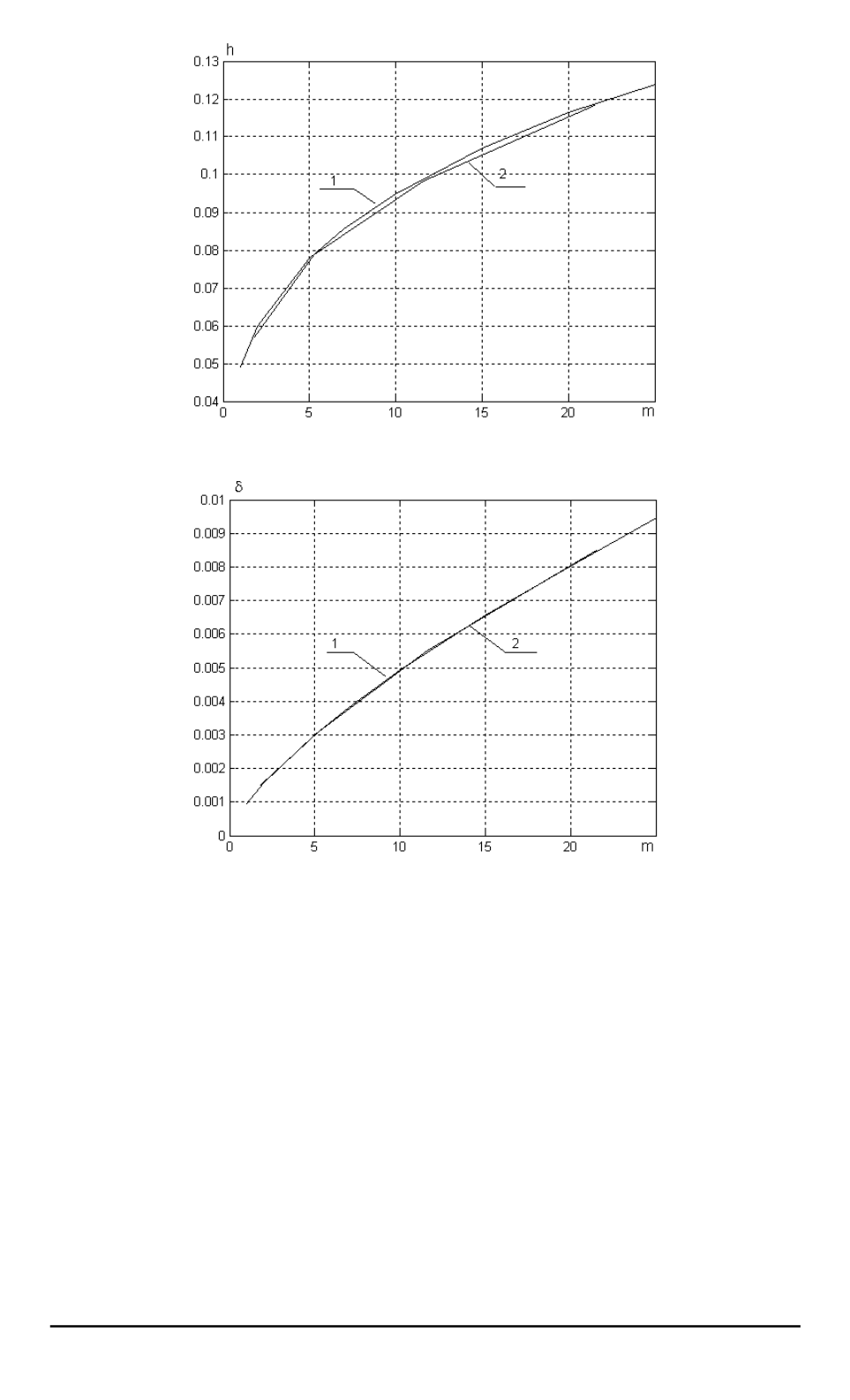
Рис. 9. Функция
h
(
m
)
:
1
— оптимизация по потоку;
2
— оптимизация по массе
Рис. 10. Функция
δ
(
m
)
:
1
— оптимизация по потоку;
2
— оптимизация по массе
ребра сохраняется, а значит, наилучшие геометрические параметры
конструкции можно находить без проведения оптимизации.
СПИСОК ЛИТЕРАТУРЫ
1. А м о с о в А. А., Д у б и н с к и й Ю. А., К о п ч е н о в а Н. В. Вычисли-
тельные методы для инженеров. – М.: Высш. шк., 1994. – 544 с.
2. З а р у б и н В. С. Математическое моделирование в технике. / Под ред.
В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. –
496 с.
3. З а р у б и н В. С. Температурные поля в конструкции летательных аппаратов.
– М.: Машиностроение, 1966. – 216 с.
4. З и г е л ь Р., Х а у э л л Д ж. Теплообмен излучением: Пер. с англ. – М.:
Мир, 1975. – 934 с.
5. К е р н Д., К р а у с А. Развитые поверхности теплообмена: Пер. с англ. –
М.: Энергия, 1977. – 464 с.
40
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3


