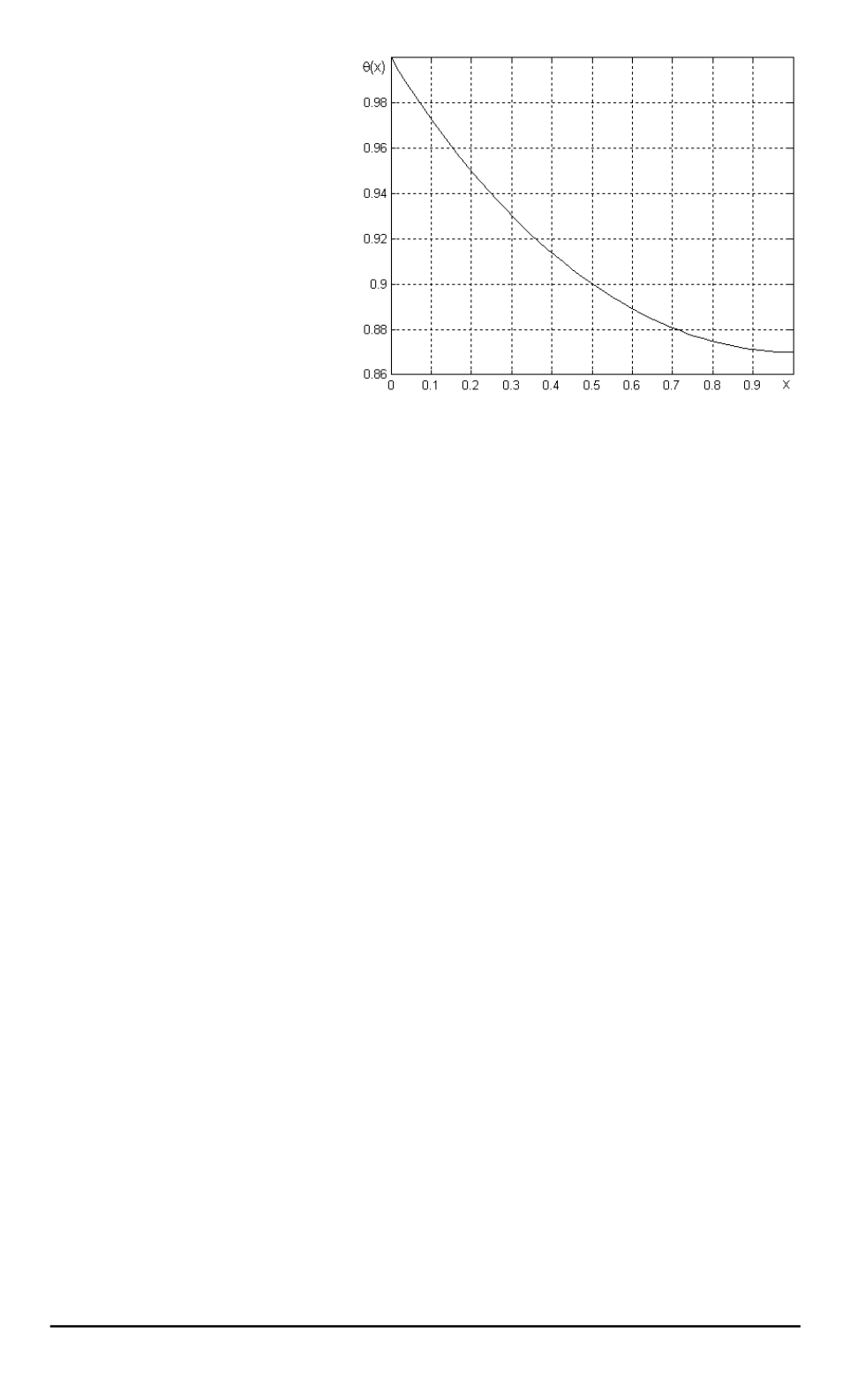
Рис. 3. Распределение температуры по высоте
ребра
часть уравнения (1). Затем
проводится решение этого
дифференциального урав-
нения, в результате чего
получается распределение
температуры
θ
(
x
)
, с по-
мощью которого определя-
ются новые распределения
q
БП
(
u
)
и
q
P
(
x
)
.
Далее порядок расчeта
повторяется; для заверше-
ния цикла использовано
условие
Q
(
k
)
−
Q
(
k
−
1)
≤
,
где
Q
=
Q
P
+
Q
БП
+
Q
T
— суммарный тепловой поток, полученный с по-
мощью формул (8)–(10);
k
— номер итерации; — точность основного
итерационного метода.
Рассмотрим конструкцию с параметрами:
ρ
= 2670
кг/м
3
,
λ
=
= 203
Вт/(м
∙
K),
ε
= 0
,
88
,
R
= 0
,
1
м,
ε
0
= 0
,
5
. Для
N
= 5
, N
c
= 0
,
5
,
T
0
= 1000
K и суммарной массы рeбер
m
= 10
кг распределение тем-
пературы по высоте ребра приведено на рис. 3.
Оптимизация конструкции.
Так как наличие рeбер увеличивает
массу теплообменного устройства, нужно оптимизировать их число
и геометрические характеристики. Если задан материал, из которого
сделаны рeбра, а также радиус трубы, то имеется пять неопределeнных
параметров математической модели: масса
m
, число рeбер
N
, высота
h
и толщина
2
δ
ребра, а также излучаемый с поверхности конструкции
тепловой поток
Q
. При введении безразмерного параметра
N
c
(см. (1))
число параметров сокращается до четырeх. В данной модели
m, N, N
c
— внутренние параметры, а
Q
— выходной параметр.
Если задана суммарная масса рeбер, то условие максимума излу-
чаемого теплового потока можно записать в виде
Q
=
F
(
N, N
c
)
−→
max
,
где
F
— указанная выше связь между этими величинами. Однако пара-
метр
N
— дискретный, и поэтому удобнее, задавая различные значения
N
, решать задачу одномерной оптимизации:
Q
=
F
(
N
c
)
−→
max
.
(11)
Если же задан суммарный излучаемый поток, то необходимо ре-
шать обратную задачу, т.е. по значению выходного параметра опре-
делять внутренний. Тогда условие минимума суммарной массы имеет
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
33


