вид
m
=
G
(
N
c
)
−→
min
,
(12)
где
G
— неизвестная функция связи между этими параметрами.
Выражения для массы ребер
m
= 2
δhLNρ
(13)
и для безразмерного параметра
N
c
=
εσ
λδ
h
2
T
3
0
(14)
при заданных значениях
m
и
N
c
представляют собой систему для
определения геометрических характеристик ребра
h
и
δ
.
Рассмотрим задачу одномерной оптимизации (11). Объем вычисле-
ний для получения значения функции
F
очень велик, поэтому жела-
тельно обращаться к процедуре вычисления излучаемого потока воз-
можно меньшее число раз; здесь можно воспользоваться, например,
методом золотого сечения.
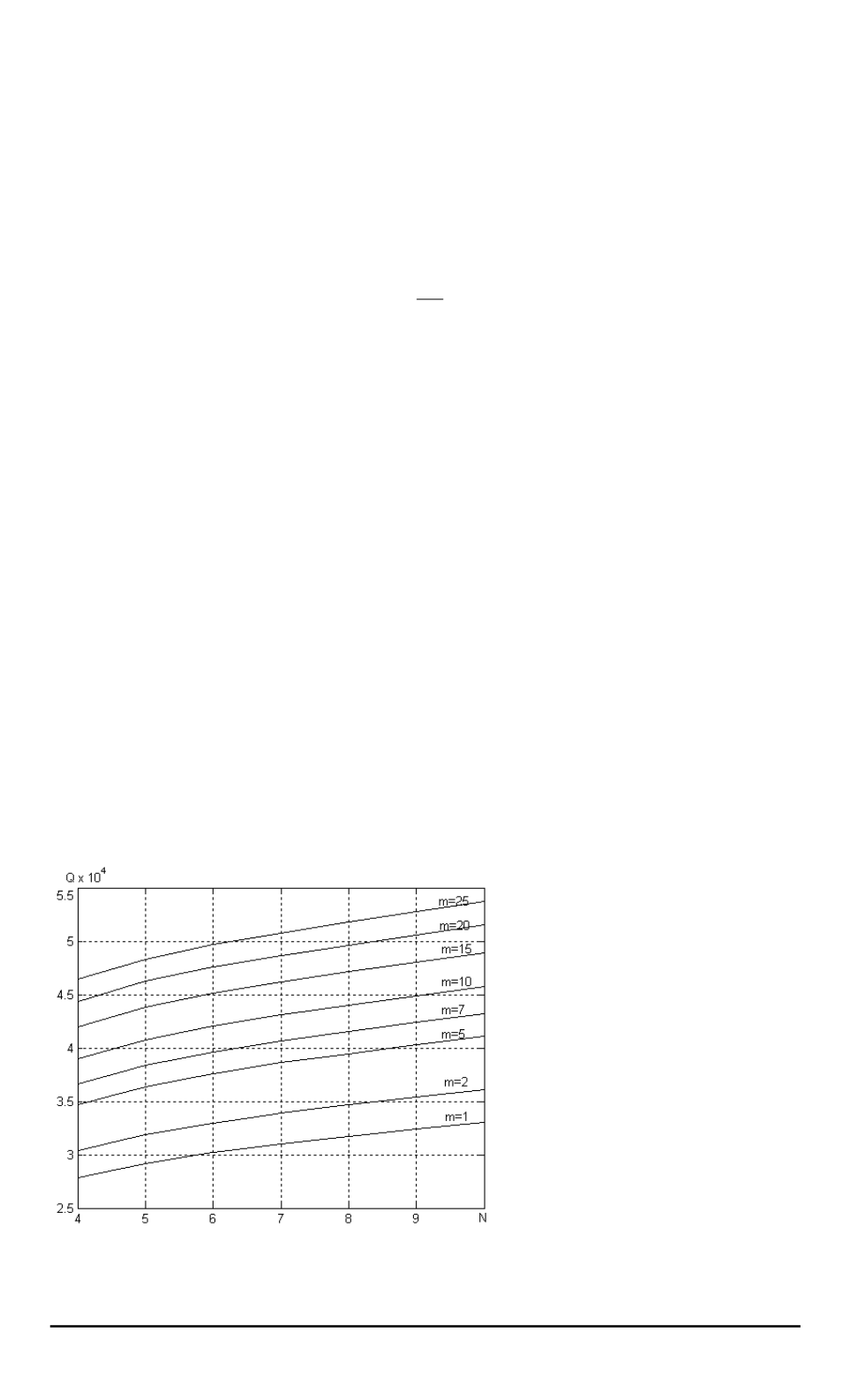
Результаты оптимизации:
Q
max
, Вт;
h
, м;
δ
, м, для различных значе-
ний массы и разного числа представлены на рис. 4–6. C ростом числа
рeбер и с уменьшением массы толщина и высота оптимального ребра,
вычисленные по формулам (13) и (14), убывают монотонно.
С увеличением массы при постоянном
N
поток излучения увели-
чивается. Это связано с увеличением объeма конструкции, а значит, и
площади еe поверхности.
При увеличении числа рeбер и постоянной массе максималь-
ный тепловой поток также увеличивается. Здесь надо учитывать
несколько факторов: 1) при увеличении
N
увеличивается суммарная
Рис. 4. Максимальный отводимый тепловой
поток
площадь поверхности рe-
бер, т.е. поток увеличива-
ется; 2) уменьшается угол
между соседними рeбра-
ми, что приводит к усиле-
нию теплообмена излуче-
нием между ними и погло-
щению каждым большей
доли теплоты, — т.е. рассе-
иваемый конструкцией те-
пловой поток уменьшает-
ся; 3) уменьшается пло-
щадь базовой поверхно-
сти, а значит, уменьшается
и тепловой поток.
34
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3


