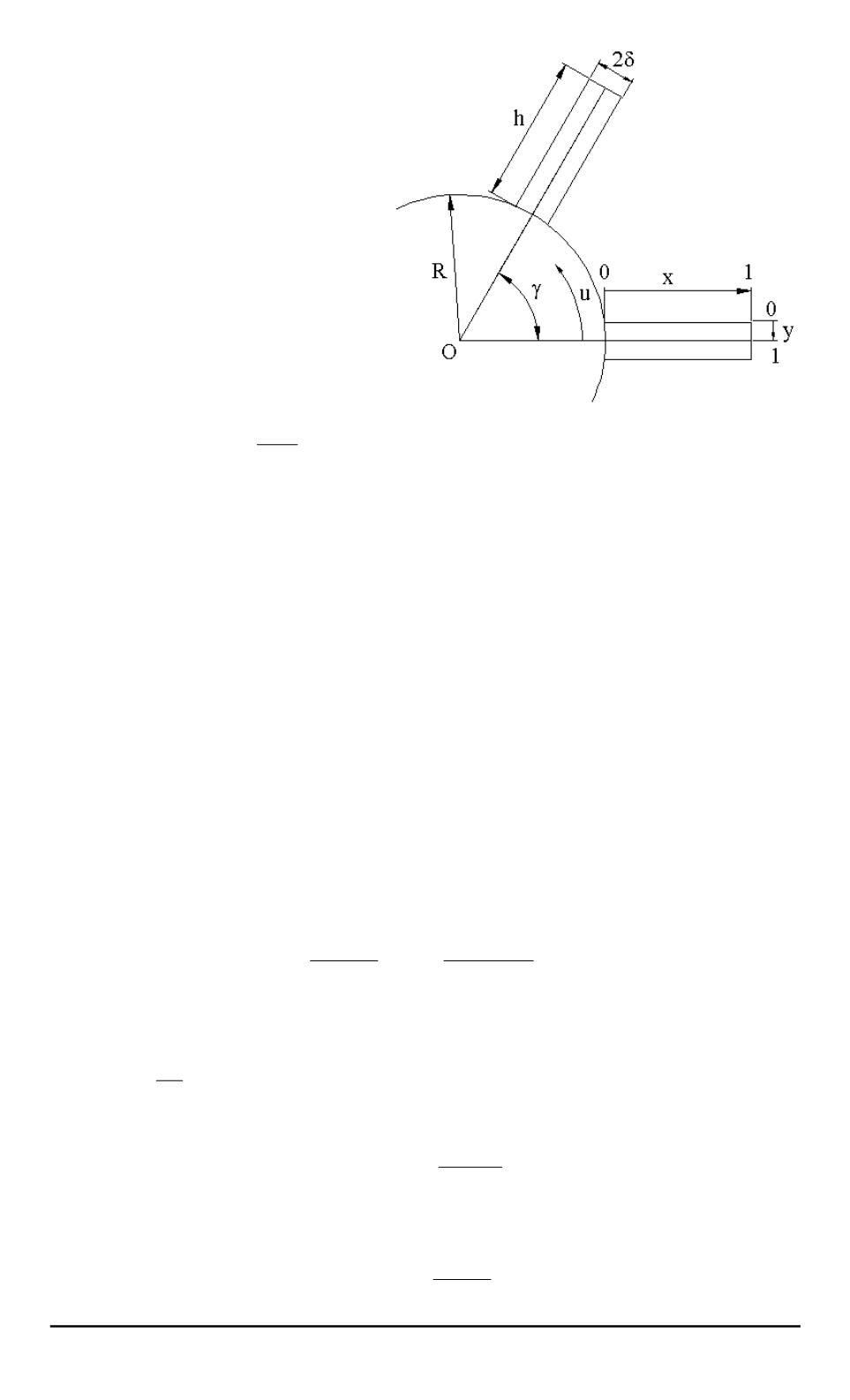
Рис. 1. Схема конструкции
Математическая мо-
дель.
В стационарных усло-
виях закон сохранения энер-
гии для элемента ребра име-
ет форму уравнения балан-
са между переносом теплоты
теплопроводностью и излу-
чением:
dQ
тепл
+
dQ
изл
= 0
.
Для одномерной модели те-
плопроводности имеем
dQ
тепл
=
−
2
δLλ
d
2
T
d
ˉ
x
2
d
ˉ
x.
Здесь
δ
— половина толщины ребра;
L
— длина ребра, принимаемая
равной единице;
λ
— коэффициент теплопроводности ребра;
T
(ˉ
x
)
—
распределение температуры по высоте вдоль боковой поверхности ре-
бра;
ˉ
x
— координата по высоте ребра.
При переносе теплоты излучением
dQ
изл
= 2(
q
изл
−
q
погл
)
Ld
ˉ
x
= 2(
εσT
4
−
εq
пад
)
Ld
ˉ
x
= 2(
q
р
−
q
пад
)
Ld
ˉ
x,
где
q
изл
=
εσT
4
— собственное излучение ребра;
ε
— коэффициент
излучения ребра;
q
пад
=
q
пад
Р(1)
+
q
пад
БП
— излучение, падающее на ребро
с другого ребра (
q
пад
P(1)
) и базовой поверхности (
q
пад
БП
);
σ
— постоянная
Стефана–Больцмана;
q
p
=
εσT
4
+(1
−
ε
)
q
пад
— эффективное излучение
ребра.
Введя безразмерные величины
x
= ˉ
x/h
,
x
2
[0
,
1]
,
θ
(
x
) =
T
(ˉ
x
)
/T
0
,
где
h
— высота ребра, а
T
0
— температура базовой поверхности, полу-
чим
d
2
θ
(
x
)
dx
2
=
N
c
q
p
−
q
пад
εσT
4
0
,
(1)
q
p
(
x
) =
εσT
4
0
θ
4
(
x
) + (1
−
ε
)
q
пад
(
x
)
,
(2)
где
N
c
=
εσ
λδ
h
2
T
3
0
— безразмерный коэффициент. Справедливы следу-
ющие граничные условия:
T
(ˉ
x
)
ˉ
x
=0
=
T
0
,
dT
(ˉ
x
)
d
ˉ
x
ˉ
x
=
h
= 0
,
или в безразмерном виде:
θ
(
x
)
x
=0
= 1
,
dθ
(
x
)
dx
x
=1
= 0
.
(3)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
29


