Математическое моделирование процессов затвердевания металлов в условиях высокоинтенсивного охлаждения - page 10

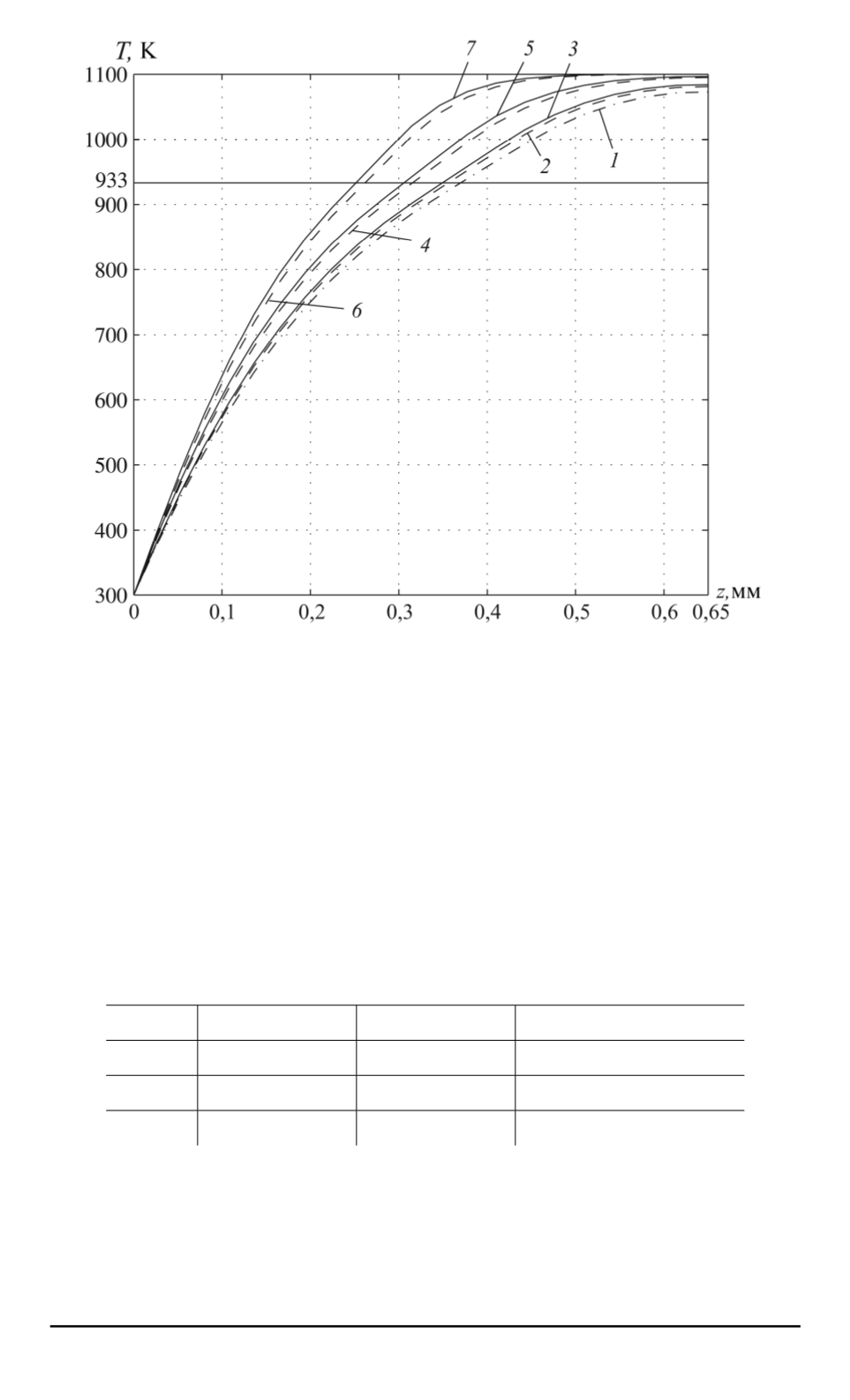
Рис. 4. Распределение температуры по оси капли:
1 — модель без учета параметров состояния, t = 4,49642∙ 10−4 с; 2 — модель с учетом
параметров состояния, t = 4,50217 ∙ 10− 4 с, τT /tз = 10− 6, τ S /tз = 10 −6; 3 — модель
с учетом параметров состояния, t = 4,50115 ∙ 10−4 с, τT /tз = 10− 6, τ S/tз = 1;
4 — модель с учетом параметров состояния, t = 4 ,49924 ∙ 10− 4 с, τT /tз = 10 −3,
τS /tз = 10 −6; 5 — модель с учетом параметров состояния, t = 4 , 49014 ∙ 10−4 с,
τT /tз = 10−3 , τS /tз = 1; 6 — модель с учетом параметров состояния, t = 4, 50125 ∙
∙ 10−4 с, τT /tз = 1, τS /tз = 10−6; 7 — модель с учетом параметров состояния,
t = 4, 50223 ∙ 10−4 с, τ T /tз = 1, τS /tз = 1
для модели с учетом параметров состояния при различных значениях
времен релаксации этих параметров.
Таблица 2
Время затвердевания капли для уточненной модели
τT /t3 τS /tз = 10−6 τS /tз = 10−3 τ S/tз = 1
10−6 0,000931083 0,000969864 0,001015082
10−3 0,001078104 0,001118245 0,001173212
1 0,001224507 0,001278568 0,00133012
Проведенные расчеты показали, что на развитие процесса суще-
ственное влияние оказывает время релаксации термодинамической
температуры. Это подтверждает положение о сильной неравновес-
ности рассматриваемого процесса. В то же время параметр порядка
оказывает менее заметное влияние на течение процесса.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3 51