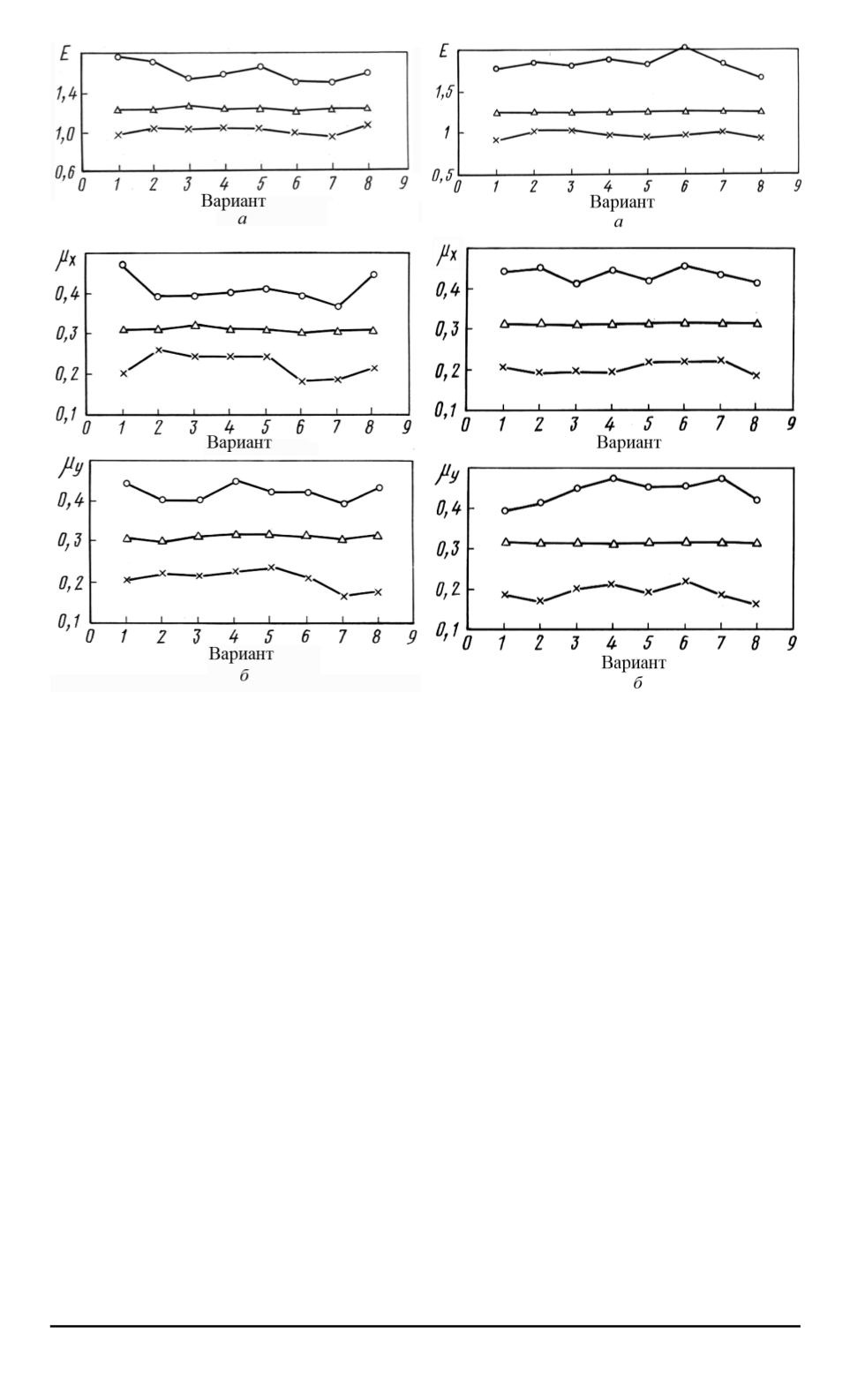
Рис. 10. Зависимость модуля Юнга
E
(
а
) и коэффициентов Пуассона
μ
x
,
μ
y
(
б
) от варианта распределения при
N
= 4
:
×
—
min
;
◦
—
max
;
M
—
avg
Рис. 11. Зависимость модуля Юнга
E
(
а
) и коэффициентов Пуассона
μ
x
,
μ
y
(
б
) от варианта распределения при
N
= 10
:
×
—
min
;
◦
—
max
;
M
—
avg
Для графиков
avg
(
E
)
, avg
(
μ
x
)
, avg
(
μ
y
)
, изображенных на рис. 10,
получаем
ε
(
E
N
=4
) = 0
,
046
, ε
(
μ
x
N
=4
) = 0
,
07
, ε
(
μ
y
N
=4
) = 0
,
07
,
а для соответствующих графиков в случае
N
= 10
имеем (см. рис. 11)
ε
(
E
N
=10
) = 0
,
011
, ε
(
μ
x
N
=10
) = 0
,
012
, ε
(
μ
y
N
=10
) = 0
,
011
.
Таким образом, для области, состоящей из 1000 СЭ, влияние раз-
личных вариантов распределений СЭ по области на среднее значение
упругого параметра минимально.
Заключение.
Разработанный алгоритм МКСЭ применен для ре-
шения задачи теории упругости композиционных материалов в трех-
мерном случае. Для решения задачи разработан программно-вычисли-
тельный комплекс, позволяющий в автоматизированном режиме про-
водить расчеты упругих параметров композиционных материалов.
66
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3


