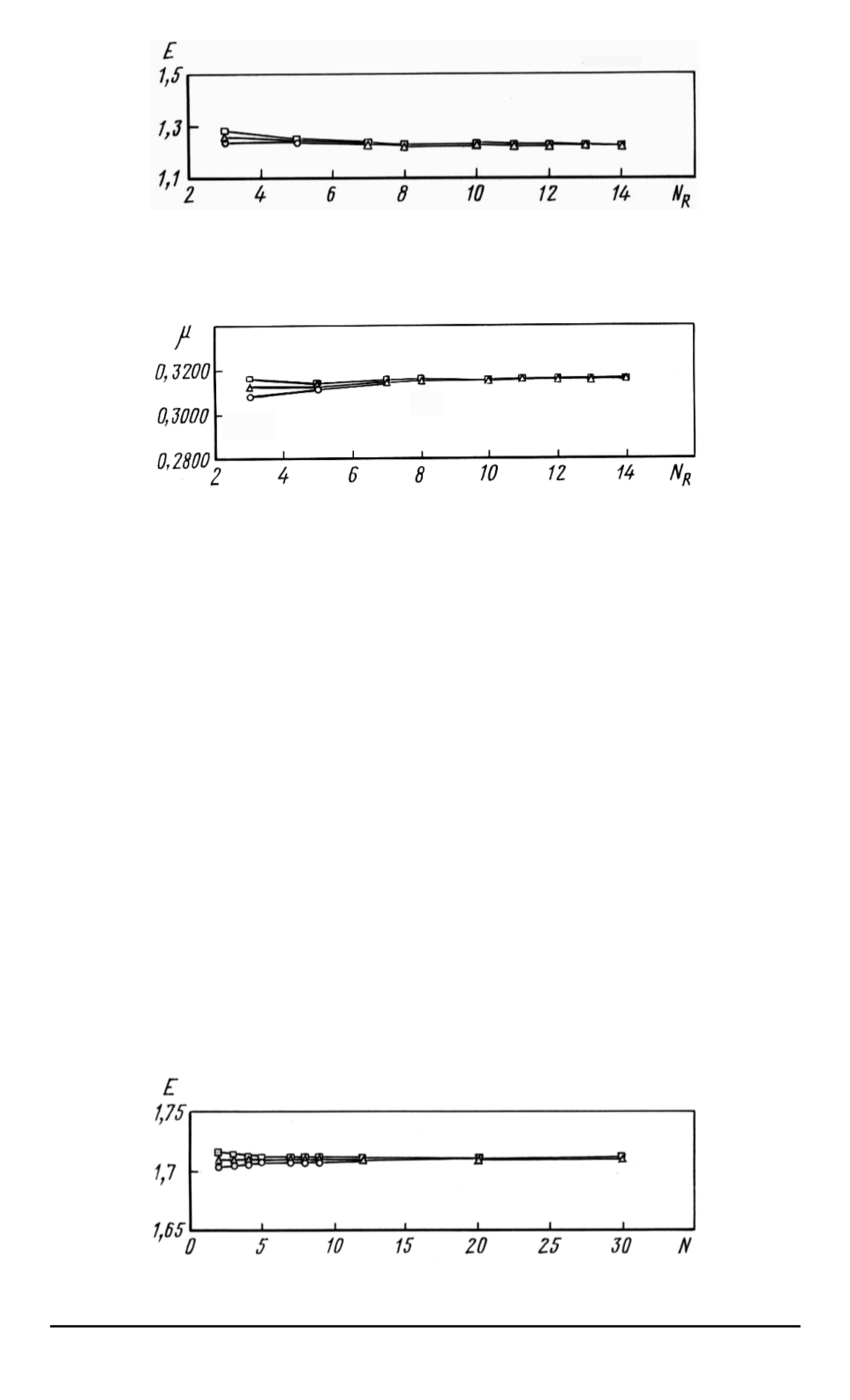
Рис. 6. Зависимость модуля Юнга композита от числа разбиений ребра СЭ
E
(
N
R
)
:
◦
—
min
; —
max
;
M
—
avg
Рис. 7. Зависимость коэффициента Пуассона композита от числа разбиений ре-
бра СЭ:
◦
—
min
; —
max
;
M
—
avg
Разный размер расчетной области.
Пусть расчетная область состо-
ит из
N
×
N
×
N
СЭ, где
N
изменяется в диапазоне 2. . . 30, а общее
число СЭ в области изменяется в диапазоне 8. . . 27000. Радиус включе-
ния
R
= 0
,
4
. Как и в других расчетах, параметры материалов матри-
цы и включений имеют следующие значения:
E
m
= 1
,
0
, E
f
= 6
,
5
,
μ
m
= 0
,
33
, μ
f
= 0
,
25
; число разбиений ребра ячейки СЭ
N
R
= 10
.
Чтобы избежать влияния распределения СЭ, все расчеты проводились
для одного фиксированного типа СЭ.
На рис. 8–9 приведены графики зависимостей приведенных упру-
гих параметров композитного тела от параметра
N
. Как видно на
рисунках, с увеличением
N
происходит сужение интервала
[min; max]
(это следует из увеличения размеров области и числа СЭ, по которым
происходит усреднение) и плавное незначительное изменение средних
значений — увеличение
E
и уменьшение
μ
.
Рис. 8. Зависимость модуля Юнга композита от параметра
N
:
◦
—
min
; —
max
;
M
—
avg
64
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3


