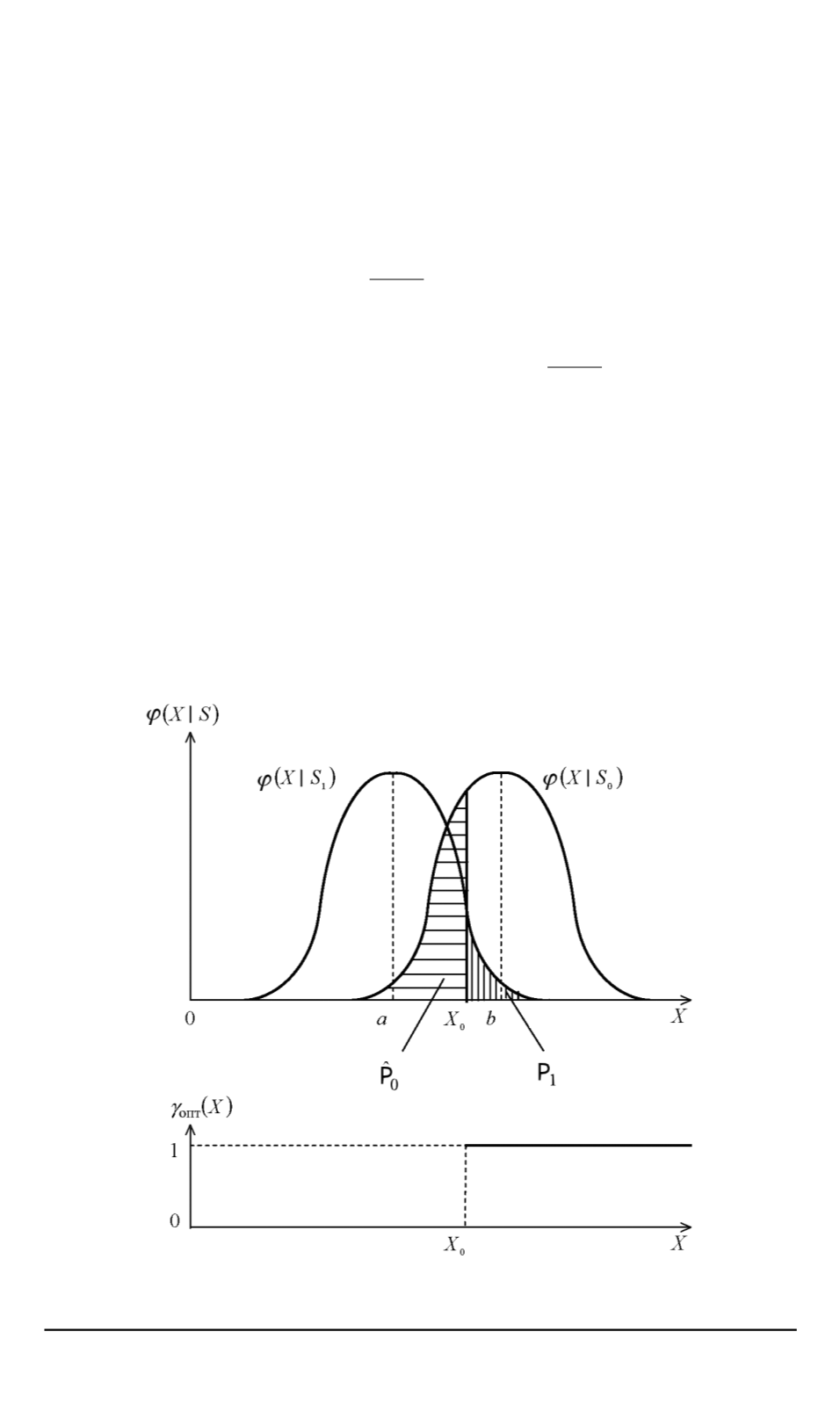
Анализ рис. 1 показывает, что
ˆ
P
0
зависит не только от величины
выбранного порога
X
0
, но и от разности
b
−
a
и волатильности
σ
.
Чем больше разность
b
−
a
, тем меньше значение
ˆ
P
0
. Чем меньше
волатильность характеристик заемщиков
σ
, тем меньше значение
ˆ
P
0
(при той же самой разности
b
−
a
)
. Для вычисления
ˆ
P
0
необходимо
использовать выражения (8), (9). При этом имеем
ˆ
P
0
= 0
,
5 +
N
b
−
a
σ
−
N
−
1
(0
,
5
−
P
1
)
.
Семейство зависимостей
ˆ
P
0
от параметра
b
−
a
σ
при фиксирован-
ных значениях
P
1
и для случая применения оптимальной функции
решения
γ
опт
(
X
)
по аналогии с [3] может быть названо семейством
кривых оптимального управления кредитным риском. На рис. 2 в ка-
честве примера представлено семейство кривых оптимального упра-
вления кредитным риском для значений
P
1
, равных 0,01; 0,05 и 0,1.
С помощью рассматриваемого семейства кривых можно оценить
минимально достижимый уровень кредитного риска при заданном
пороге
X
0
. Для этого необходимо иметь параметры распределений
ϕ
(
X
|
S
0
)
и
ϕ
(
X
|
S
1
)
, т. е.
a
,
b
и
σ
, а также величины потерь
h
01
и
h
10
Рис. 1. Условные плотности вероятности
ϕ
(
X
|
S
0
)
,
ϕ
(
X
|
S
1
)
и функция реше-
ния
γ
опт
(
X
)
116
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 1


