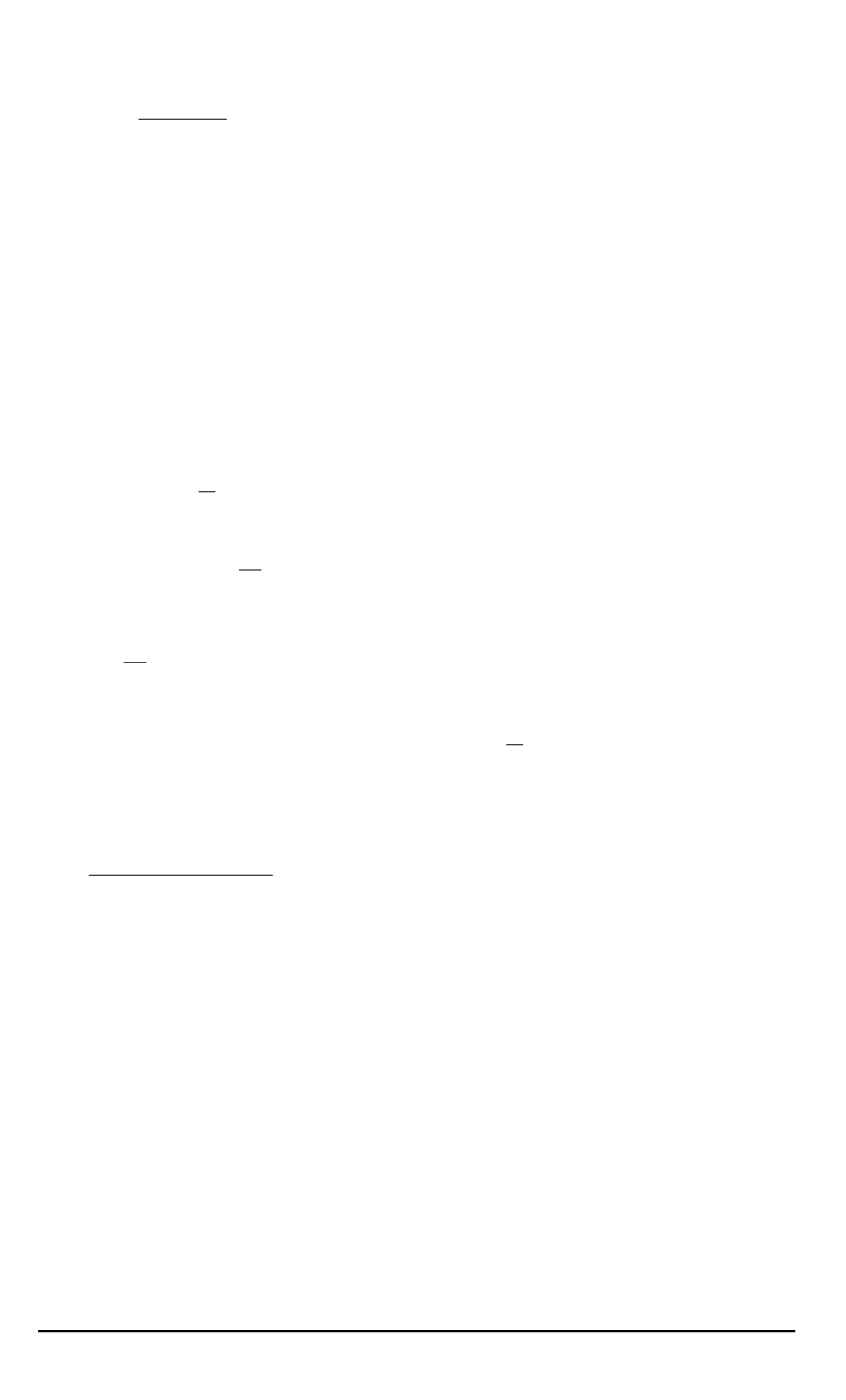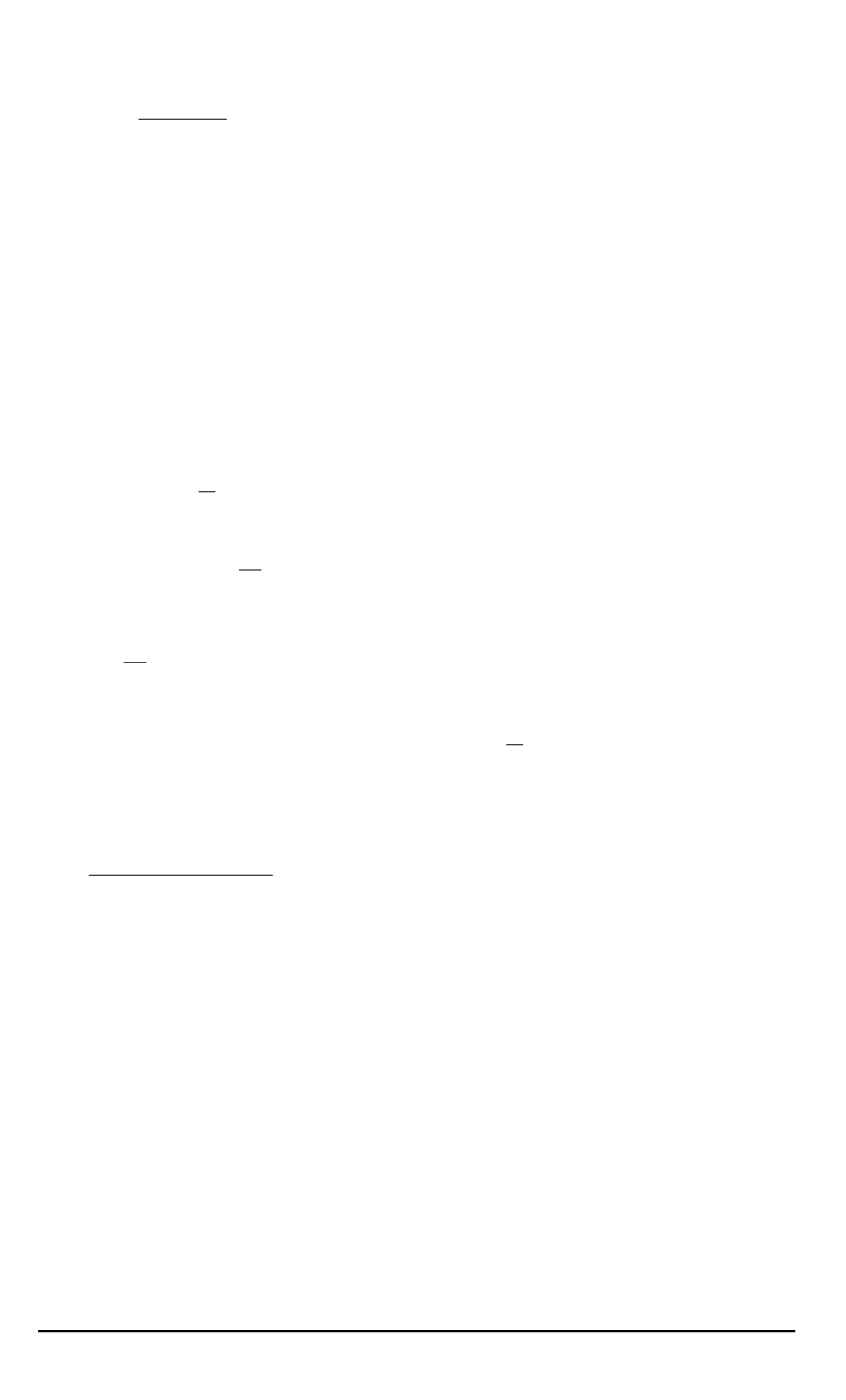
получим
∂K
(
t, s
)
∂s
=
c
0
1
(
s
)
y
1
(
t
) +
c
0
2
(
s
)
y
2
(
t
) +
. . .
+
c
0
n
(
s
)
y
n
(
t
)
.
(
7
)
2.
Далее будет использоваться следующая
Лемма
.
Пусть
ϕ
(
t
)
,
0
6
t <
∞
, —
n
раз непрерывно дифференци
-
руемая функция
.
Если при всех
t
выполняется неравенство
¯ ¯
ϕ
(
n
)
(
t
)
¯ ¯
6
C
¡
|
ϕ
(
t
)
|
+
|
ϕ
0
(
t
)
|
+
. . .
+
¯ ¯
ϕ
(
n
−
1)
(
t
)
¯ ¯ ¢
,
(
8
)
то
ϕ
(
t
)
, ϕ
0
(
t
)
, . . . , ϕ
(
n
−
1)
(
t
) (
следовательно
,
и
ϕ
(
n
)
(
t
))
—
функции экс
-
поненциального типа
.
Доказательство леммы
.
Введем вектор
-
функцию
¯
ϕ
(
t
)
с координа
-
тами
¡
ϕ
(
t
)
, ϕ
0
(
t
)
, . . . , ϕ
(
n
−
1)
(
t
)
¢
и нормой
k
ϕ
(
t
)
k
=
|
ϕ
(
t
)
|
+
|
ϕ
0
(
t
)
|
+
. . .
+
¯ ¯
ϕ
(
n
−
1)
(
t
)
¯ ¯
.
Имеем
ϕ
0
(
t
) =
¡
ϕ
0
(
t
)
, ϕ
00
(
t
)
, . . . , ϕ
(
n
)
(
t
)
¢
,
°°
ϕ
0
(
t
)
°°
=
|
ϕ
0
(
t
)
|
+
|
ϕ
00
(
t
)
|
+
. . .
+
¯ ¯
ϕ
(
n
−
1)
(
t
)
¯ ¯
+
¯ ¯
ϕ
(
n
)
(
t
)
¯ ¯
6
6
(
C
+ 1)
¡
|
ϕ
0
(
t
)
|
+
|
ϕ
00
(
t
)
|
+
. . .
+
¯ ¯
ϕ
(
n
−
1)
(
t
)
¯ ¯ ¢
+
+
C
|
ϕ
(
t
)
|
6
D
k
ϕ
(
t
)
k
, D
=
C
+ 1
.
Пусть
ϕ
0
—
положительное число
,
не меньше
,
чем
k
¯
ϕ
(
t
0
)
k
.
Тогда
¯
ϕ
(
t
0
+
h
)
−
¯
ϕ
(
t
0
)
h
=
ϕ
0
(
t
0
) + ¯
α
(
h
)
,
k
¯
α
(
h
)
k →
0
при
h
→
0
.
Поэтому при
h >
0
получим
k
¯
ϕ
(
t
0
+
h
)
k
6
ϕ
0
+
Dϕ
0
h
+
k
¯
α
(
h
)
k
h.
Существует
δ >
0
такое
,
что при
h
≤
δ
имеем
k
¯
α
(
h
)
k
6
Dϕ
0
.
Следовательно
,
k
¯
ϕ
(
t
0
+
h
)
k
=
k
¯
ϕ
(
t
)
k
6
ϕ
0
(1 + 2
Dh
)
6
ϕ
0
e
2
Dh
=
ϕ
0
e
2
D
(
t
−
t
0
)
(
9
)
при
t
0
6
t
6
t
0
+
δ
.
В частности
,
при
h
=
δ
имеем
k
¯
ϕ
(
t
0
+
δ
)
k
6
ϕ
0
e
2
Dδ
.
(
10
)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
33