K
(
t
−
τ
) =
∞
X
n
=1
u
n
(
t
−
τ
)
,
(21)
в котором
u
n
+1
(
t
−
τ
) =
−
t
Z
τ
u
1
(
t
−
s
)
u
n
(
s
−
τ
)
ds
;
(22)
u
1
(
t
−
τ
) =
3
κ
c
V
R
√
πχ
1
√
t
−
τ
+
√
πχ
R
.
(23)
Расчет по формуле (22) показывает, что для не слишком больших
значений
t
−
τ
ряд (21) с хорошей степенью точности может быть
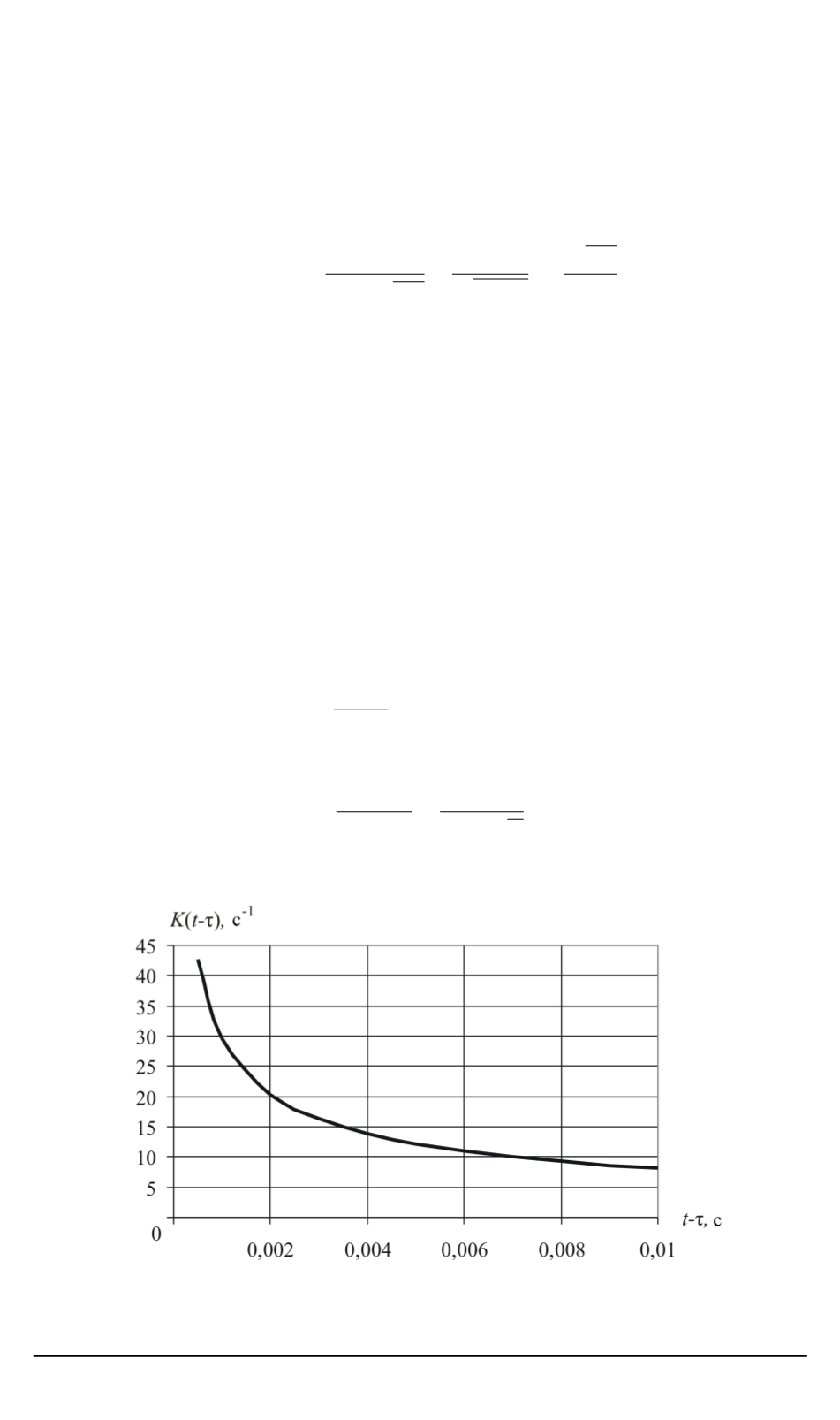
определен с помощью суммы первых его членов. На рис. 2 изображен
схематический график функции
K
(
t
−
τ
)
в случае, если сохранены
первые 10 слагаемых (для простоты все постоянные приняты за еди-
ницу). Хорошо видно, что построенный график представляет убыва-
ющую функцию. Аппроксимируя его степенной функцией, получаем
в хорошем приближении зависимость
K
(
t
−
τ
) = 0
,
61(
t
−
τ
)
−
0
,
57
.
(24)
В частном случае теплопроводности над плоскостью (при
R
=
∞
)
ряд (21) принимает вид [8]
K
(
t
−
τ
) =
1
t
−
τ
∞
X
n
=1
(
−
1)
n
α
n
(
t
−
τ
)
n/
2
,
(25)
где
α
n
=
1
Γ(
n/
2)
3
κ
c
V
R
√
χ
n
;
(26)
Γ(
x
)
— гамма-функция.
Рис. 2. Схематический график функции
K
(
t
−
τ
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1
73


