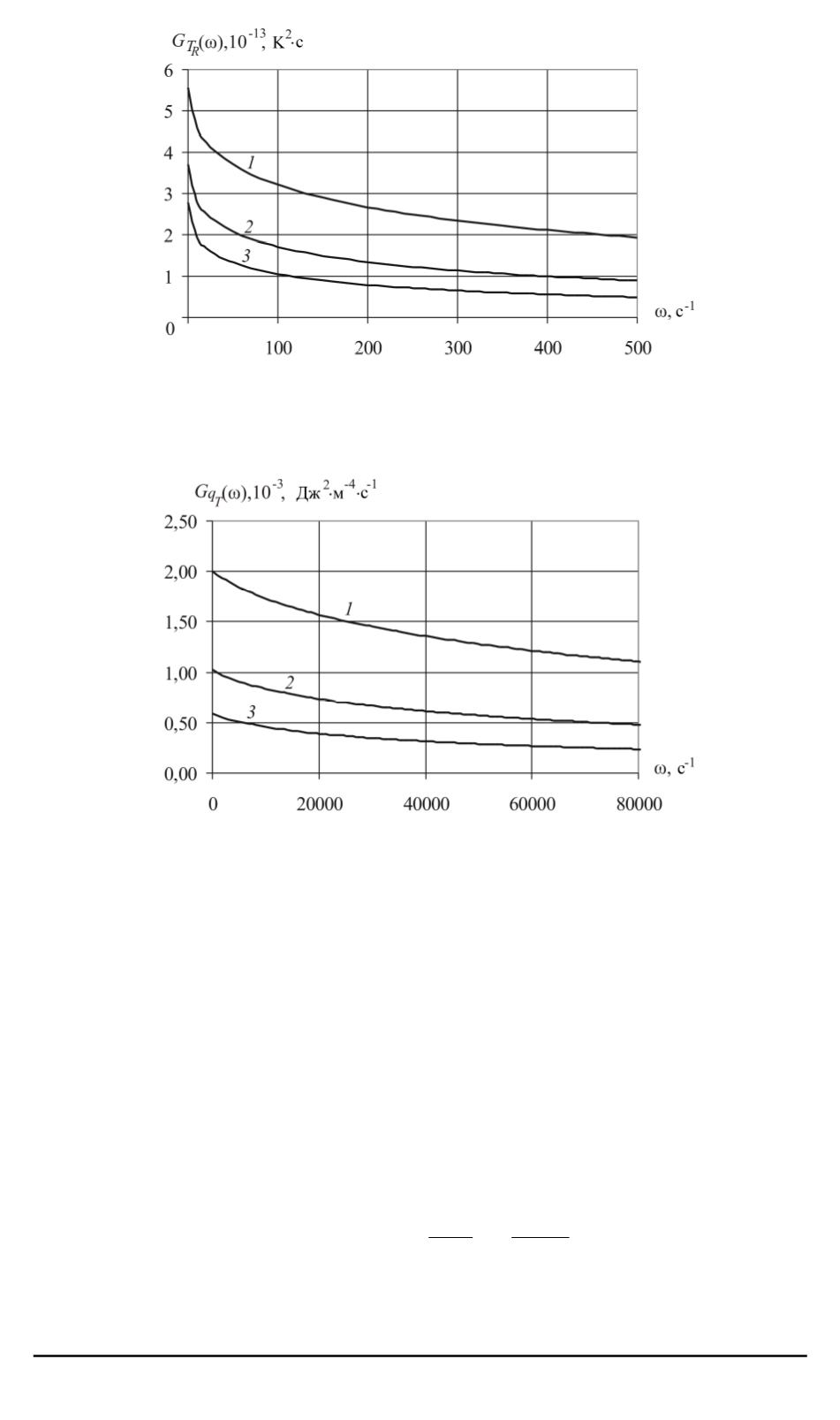
Рис. 3. Графики спектральной плотности флуктуаций температуры поверхно-
сти медной частицы
G
T
R
(
ω
)
при
R
= 10
(
1
);
R
= 12
,
5
(
2
);
R
= 15
мкм (
3
)
Рис. 4. Графики спектральной плотности флуктуаций теплового потока через
поверхность медной частицы
G
q
T
(
ω
)
при
R
= 10
(
1
);
R
= 12
,
5
(
2
);
R
= 15
мкм (
3
)
Графики на рис. 3 и 4 иллюстрируют найденные зависимости (37)
и (38) для различных значений радиуса
R
. При построении графиков
параметр
ν
рассчитывался согласно выражению (7). На рис. 3 хорошо
видно, что с увеличением радиуса
R
графики спектральной плотности
G
T
R
(
ω
)
флуктуаций температуры
T
R
(
t
)
располагаются ниже аналогич-
ных графиков, соответствующих меньшим по размеру частицам. Это
означает уменьшение дисперсии флуктуаций температуры сфериче-
ской частицы с ростом ее радиуса. Спектральная плотность
G
T
R
(
ω
)
в
области низких частот обратно пропорциональна радиусу:
G
T
R
(
ω
)
|
ω
→
0
=
R
2
ν
κ
2
k
B
T
2
κR
.
(39)
Таким образом, рассмотрение процесса теплопроводности даже в
случае относительно простых моделей (вне сферической поверхности
76
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1


