Будем предполагать
,
что элементы АС являются ненаправленны
-
ми
,
расположенными в одной горизонтальной плоскости
,
комплексные
коэффициенты передачи каналов известны
,
а взаимное влияние эле
-
ментов АС отсутствует
.
При этом имеется параметрическая априорная неопределенность
,
представляющая собой векторы неинформативных параметров
[2],
в
частности векторы параметров
~
A
и
~
ϕ
н
.
В указанных условиях априор
-
ной неопределенности векторы параметров
~
β
и
~
θ
являются информа
-
тивными и подлежат измерению в априори известных ограниченных
интервалах
£
β
min
,
β
max
¤
и
£
θ
min
,
θ
max
¤
соответственно
.
Если векторы неинформативных параметров зафиксированы
,
то ре
-
зультаты наблюдений
,
представляющие собой случайную выборку
(
ре
-
ализацию случайного процесса
),
имеют полностью определенные ве
-
роятностные характеристики
.
Тогда информация на выходе АС имеет
вид
~
x
=
~
s
+
~
w
,
(
1
)
где
~
s
=
{
s
1
,
s
2
, . . . ,
s
m
, . . . ,
s
M
}
,
s
m
=
N
∑
n
=
1
A
n
exp
(
j
(
ϕ
н
n
+
µ
m
cos
β
n
cos
(
θ
n
−
γ
m
)))
—
суммарный сигнал от всей совокупности источников излучения
,
принимаемый
m
-
м элементом АС
;
~
w
—
вектор помехи
,
имеющей нор
-
мальное распределение с нулевым математическим ожиданием и кор
-
реляционной матрицей
K
;
µ
m
=
2
π
D
m
/
λ
,
D
m
—
расстояние между
точкой привязки фазы и
m
-
м элементом АС
,
λ
—
длина волны
;
γ
m
—
угол между направлением
,
относительно которого отсчитывается ази
-
мут
,
и прямой линией
,
соединяющей точку привязки фазы и
m
-
й эле
-
мент
.
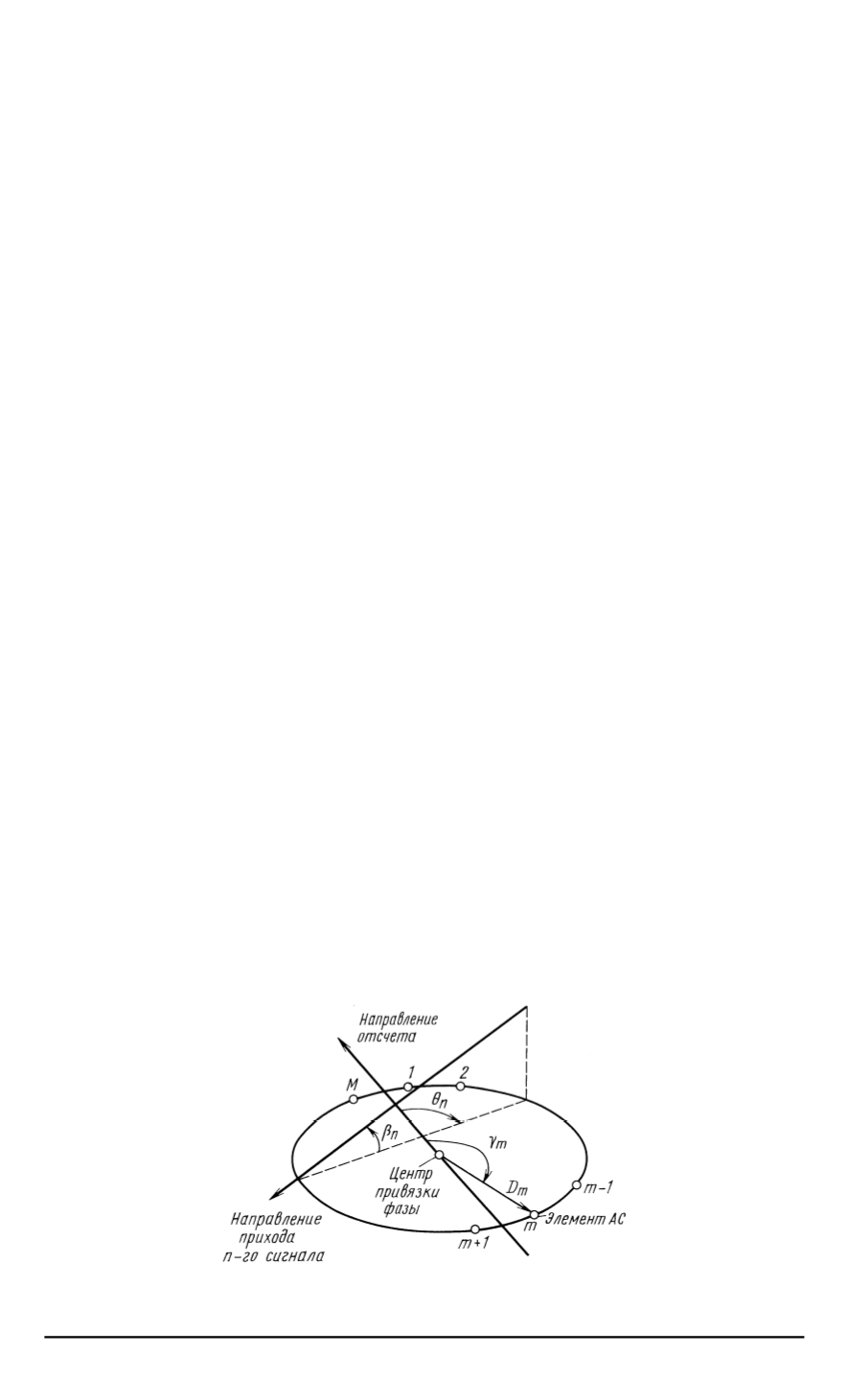
На рис
. 1
показано пространственное положение углов прихода
сигналов
(1).
Рис
. 1.
Пространственное положение углов прихода сигналов
62 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2003.
№
2


