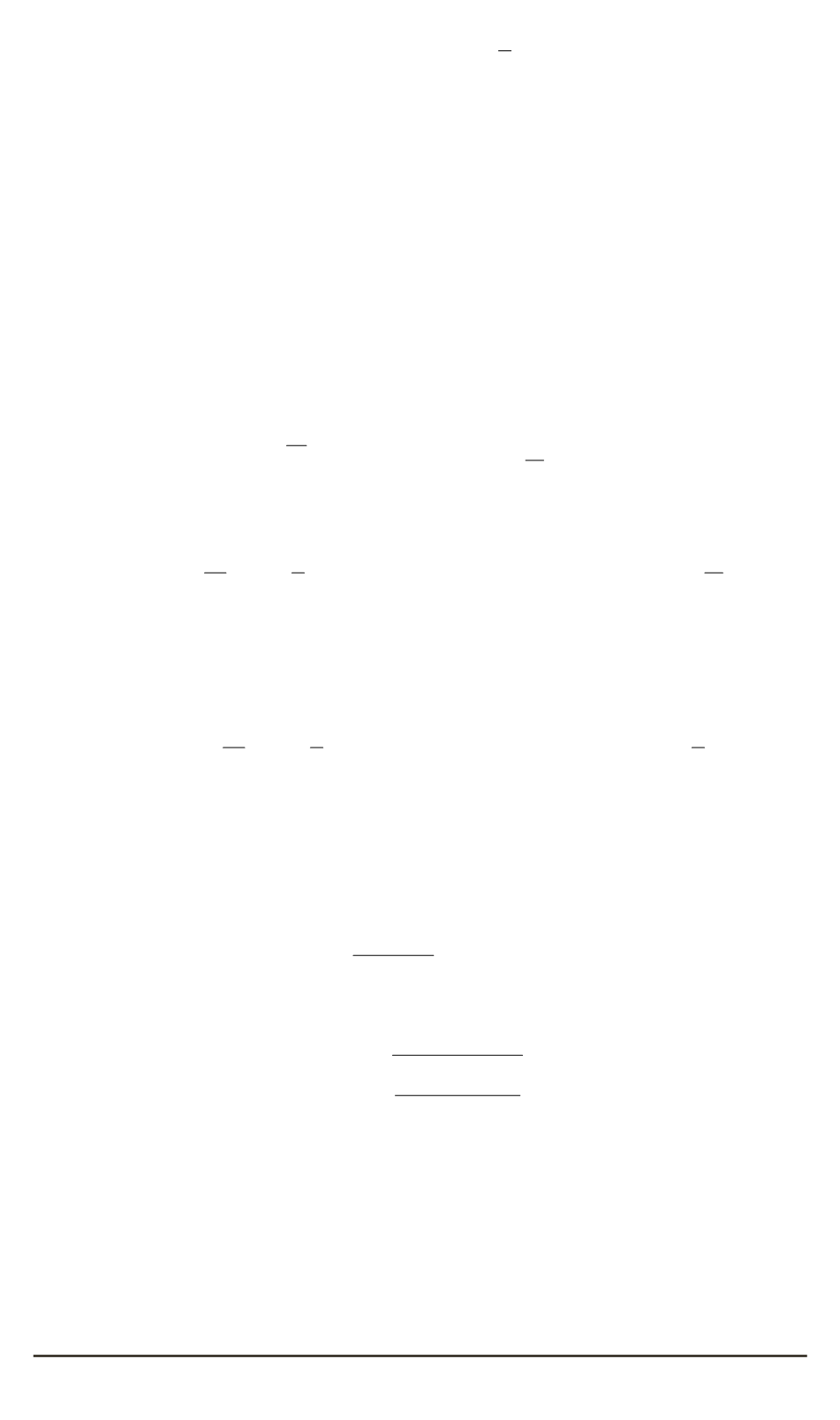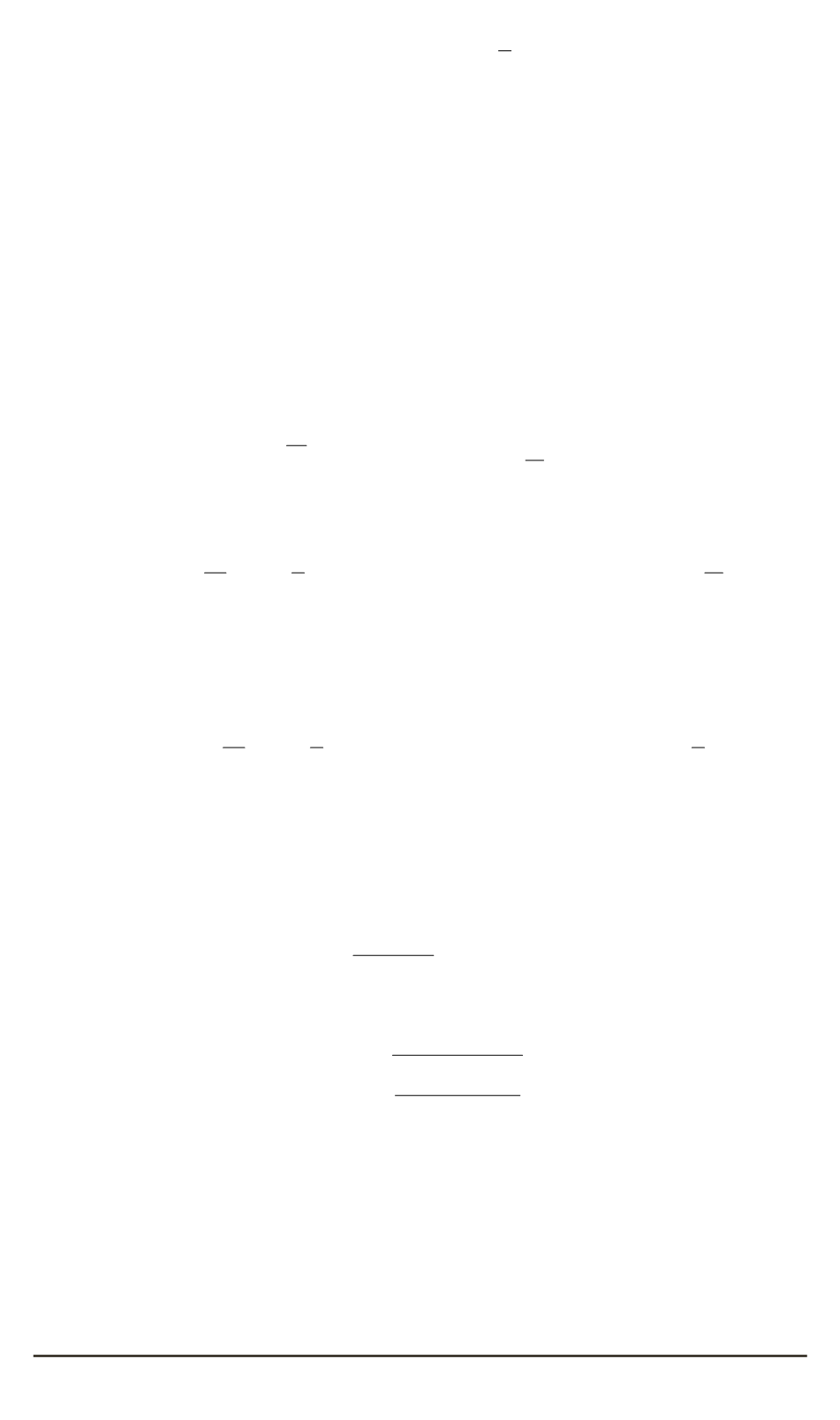
C
0
, получаем приведенное выражение;
C
h
q
2
— средние затраты на хра-
нение запасов сырья за период; если поставки товара осуществляются
партиями по
q
единиц, то средний уровень запасов за период соста-
вит
q/
2
(при равномерном расходовании сырья); учитывая затраты
C
h
на хранение единицы сырья за период, получаем, что выражение для
средних затрат на хранение единицы сырья за период имеет предста-
вленный вид (предполагается, что оплачиваются только занятые на
складе места);
C
s
(1 +
α
)
— цена за единицу сырья, по которой пред-
приятие осуществляет закупки у посредника; при этом за обработку
сырья, полученного от поставщика, посредник увеличивает стоимость
единицы сырья на наценку
α
.
Среднее изменение цены за период хранения составит
4
C
s
(
t
) =
C
s
ε
н
+
4
ε
T
2
.
Тогда суммарные издержки за период будут иметь вид
C
Σ
=
C
0
D
q
+
C
h
q
2
+
C
s
(1 +
α
)
D
−
C
s
Dε
н
−
C
s
D
4
ε
T
2
.
(1)
Период
T
между поставками можно выразить через потребление
сырья
D
за период и размер заказа
q
:
T
=
q/D
. С учетом этого формула
(1) примет вид
C
Σ
=
C
0
D
q
+
C
h
q
2
+
C
s
(1 +
α
)
D
−
C
s
Dε
н
−
C
s
4
ε
q
2
.
Оптимальный размер заказа
q
в этой модели будет соответствовать
минимуму суммарных издержек за период в точке, где производная
соответствующей функции по оптимизируемому параметру в области
q >
0
будет равна нулю:
∂C
Σ
(
q
)
∂q
= 0
.
(2)
Решение уравнения (2) дает модифицированную формулу Виль-
сона
q
=
s
2
C
0
D
C
h
−
C
s
4
ε
.
(3)
Из формулы (3) следует, что размер оптимального заказа может
быть получен при условии
4
ε < C
h
/C
s
.
Поскольку норма естественной убыли
4
ε
— постоянная величина
для конкретного вида сырья, а затраты на хранение единицы сырья
C
h
определены и зафиксированы на предприятии, управлять цепью
поставок сырья необходимо с помощью параметра
C
s
[5, 6].
124
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 4