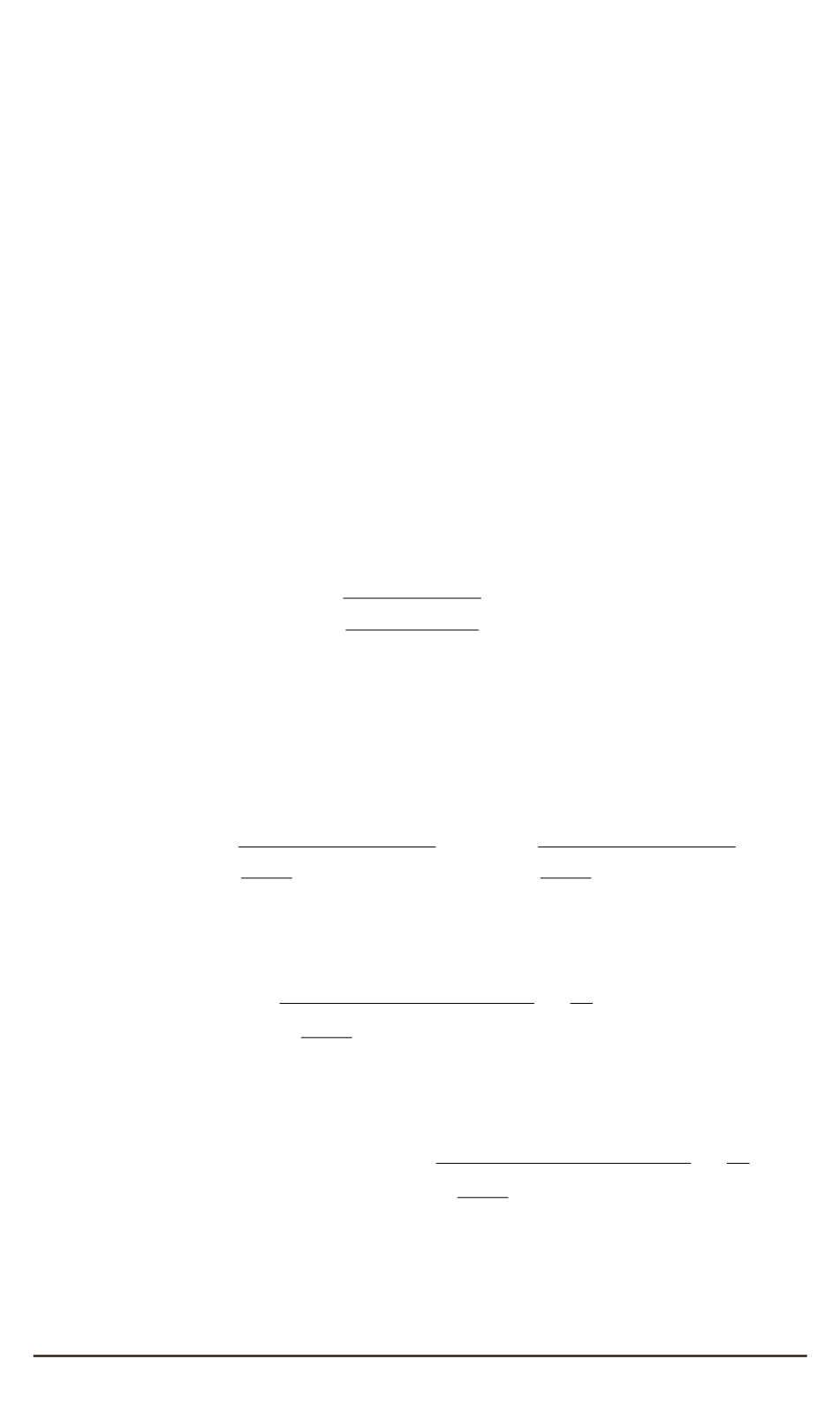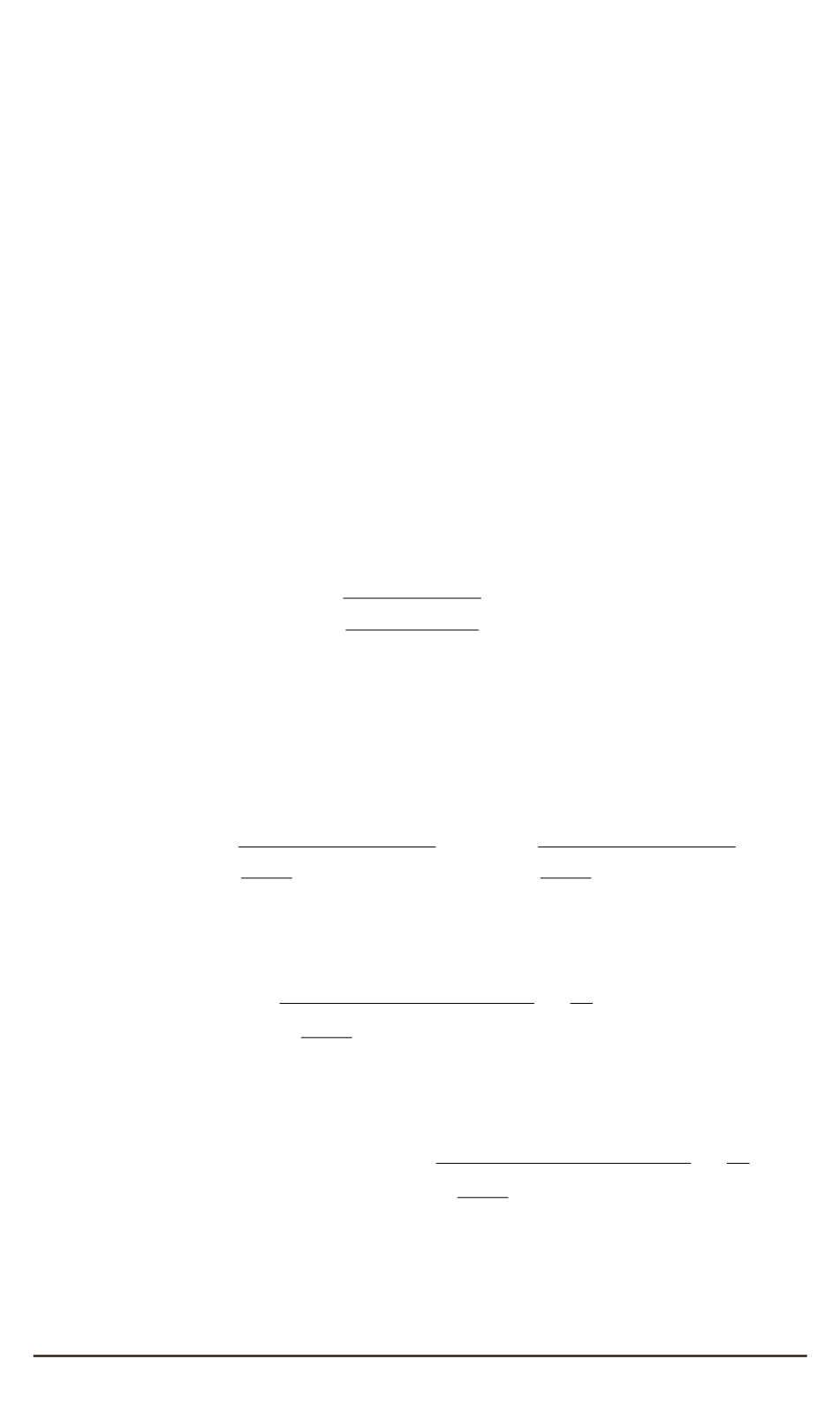
— потребление сырья за период
D
= 200
ед.;
— затраты на хранение единицы сырья за период
C
h
= 1
у.е./ед.;
— накладные расходы на каждую поставку
C
0
= 8
у.е.;
— цена закупки единицы сырья у поставщика
C
s
= 1
у.е./ед.;
— наценка фабрики группы компаний Ferrero
α
= 20
%
= 0
,
2
;
— начальное значение нормы естественной убыли
ε
н
= 0
,
015
;
— шаг изменения нормы естественной убыли
4
ε
= 0
,
004
;
— минимальный уровень суммарных затрат (в рамках принятых
понятий это означает, что суммарные затраты должны быть не
больше 2200 у.е.)
C
min
= 2200
у.е.;
— затраты на утилизацию единицы просроченного сырья
C
u
= 6
у.е.;
— значение вероятности, гарантирующей не превышение устано-
вленного уровня суммарных затрат, не менее 70%;
— время обработки сырья на фабрике группы компаний Ferrero
t
обр
= 3
дня;
— срок годности сырья
T
годн
= 45
дней.
Рассчитаем значение оптимального размера заказа по (3):
q
=
r
2
∙
8
∙
200
1
−
1
∙
0
,
004
= 56
ед
.
Подставим исходные данные в (4) и получим значение вероятно-
сти, гарантирующей не превышение установленного уровня суммар-
ных затрат:
P
C
Σ
(
t, q
) =
F
ν
2200
−
0
,
5
q
1600
q
+ 237
−
0
,
8
t
−
F
ν
1000
−
0
,
5
q
1600
q
−
963
−
0
,
8
t
=
= Φ
2200
−
0
,
5
q
1600
q
+ 237
−
0
,
8
t σ
−
m
σ
−
−
Φ
1000
−
0
,
5
q
1600
q
−
963
−
0
,
8
t σ
−
m
σ
.
Для определения параметров нормального распределения восполь-
зуемся методом точечной оценки, который предполагает нахождение
единственной величины, принимаемой за значение параметра. Такую
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 4
129