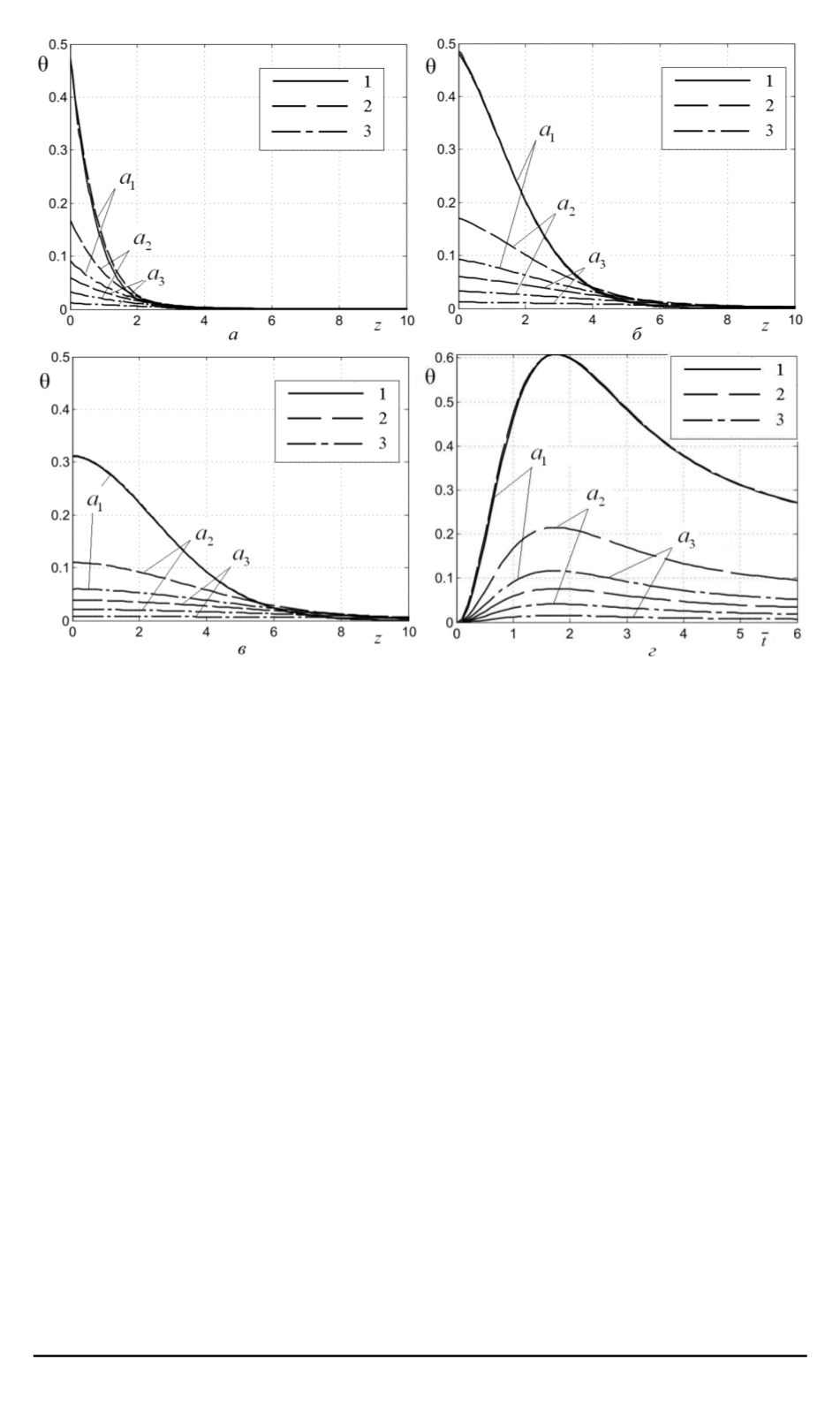
Рис. 2. Распределения температуры по глубине тела (
а–в
) и во времени для
нагреваемой поверхности тела (
г
):
1
— параболическое уравнение теплопроводности;
2
— первый вариант располо-
жения функций влияния относительно функций формы (см. рис. 1,
а
);
3
— второй
вариант (см. рис. 1,
б
);
а
—
ˉ
t
= 1
,
б
—
ˉ
t
= 3
,
в
—
ˉ
t
= 5
;
г
—
z
= 0
материале уменьшение характерного размера зерна приводит к увели-
чению доли границ раздела, а следовательно, к увеличению рассеяния
энергии на границах раздела, что соответствует понижению темпера-
туры тела.
СПИСОК ЛИТЕРАТУРЫ
1. А н д р и е в с к и й Р. А., Р а г у л я А. В. Наноструктурные материалы. – М.:
Изд. центр. “Академия”, 2005. – 192 с.
2. Г у с е в А. И. Наноматериалы, наноструктуры, нанотехнологии. – М.: ФИЗ-
МАТЛИТ, 2005. – 416 с.
3. К р и в ц о в А. М. Деформирование и разрушение твердых тел с микрострук-
турой. – М.: ФИЗМАТЛИТ, 2007. – 304 с.
4. З а р у б и н В. С., К у в ы р к и н Г. Н. Математические модели механики и
электродинамики сплошной среды. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2008.
– 512 с.
5. З а р у б и н В. С., К у в ы р к и н Г. Н. Математическое моделирование термо-
механических процессов при интенсивном тепловом воздействии // Теплофи-
зика высоких температур. – 2003. – Т. 4, № 2. – С. 300–309.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3
29


