C
k
+1
+
M
t
(
k
)
K
k
+1
T
(
k
+1)
=
M
t
(
k
)
F
(
k
+1)
+
C
k
+1
T
(
k
)
,
где
M
t
(
k
)
=
t
k
+1
−
t
k
— шаг по времени.
Для вычисления элементов
C
pq
,
K
pq
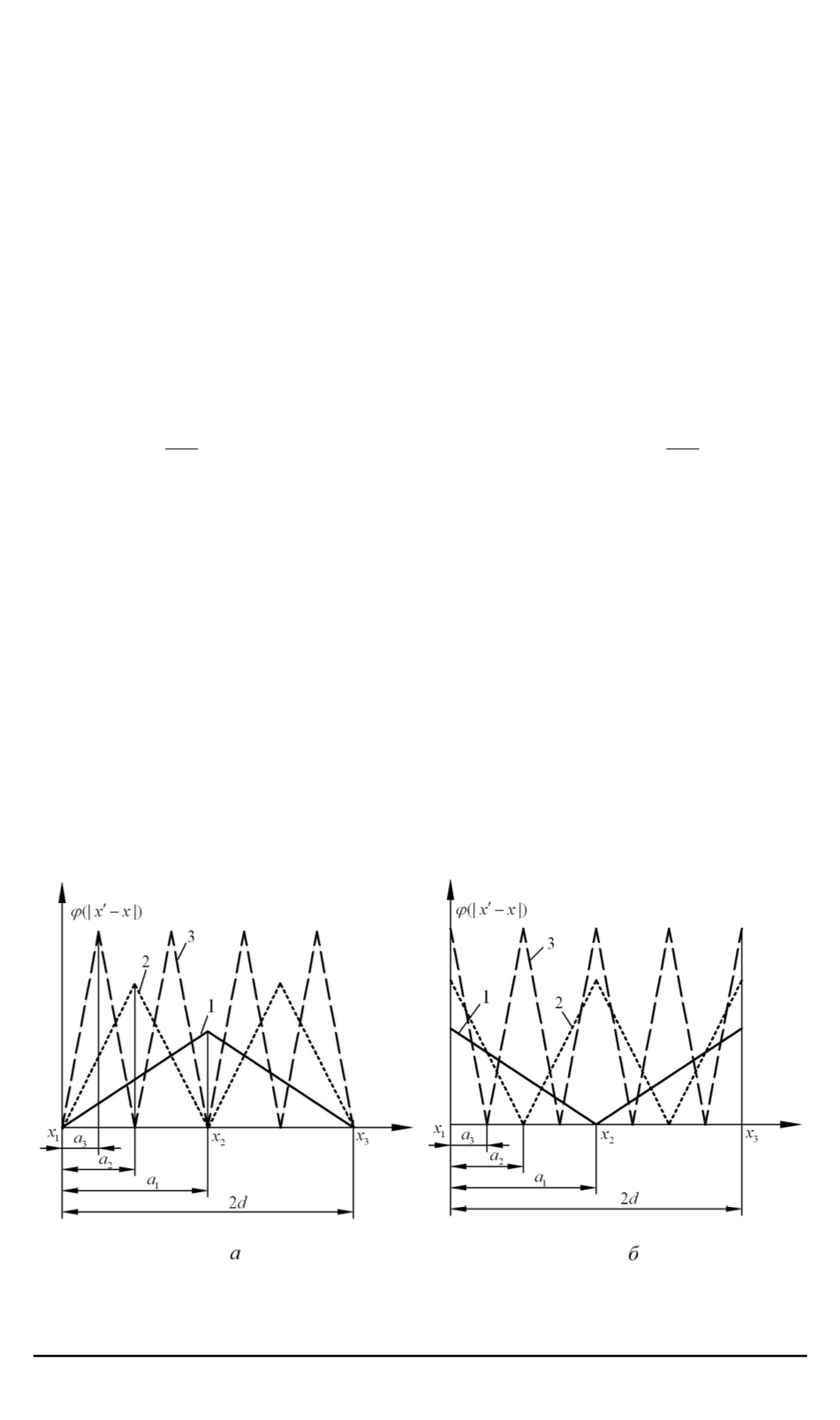
в (15) рассмотрим два вариан-
та расположения функции влияния относительно конечного элемента
(рис. 1). В первом варианте (рис. 1,
а
) максимальное значение функции
влияния достигается в центре наноструктурного элемента, во втором
(рис. 1,
б
) — на границах наноструктурного элемента.
Чтобы оценить влияние характерного размера
a
на распределение
температуры, рассмотрим случаи
a
1
=
d
,
a
2
=
d/
2
,
a
3
=
d/
4
.
При построении графиков использовали следующие безразмерные
параметры и переменные [10]:
z
=
x/
√
at
0
,
ˉ
t
=
t/t
0
, θ
= (
T
−
T
0
)
/T , T
=
Bt
0
√
at
0
.
λ
(
T
)
,
a
=
λ
(
T
)
.
(
ρc
)
, q
0
( ˉ
t
) =
M
ˉ
t
m
exp(
m
ˉ
t
)
, M
=
m
m
/
(
m
−
1)!
.
На рис. 2 изображены распределения температуры по глубине тела
для различных моментов времени (
а–в
) и расчет температуры поверх-
ности нагреваемого тела (
г
) при
m
= 2
в сравнении с температурой,
вычисленной в случае параболического уравнения теплопроводности.
Из представленных рисунков видно, что расположение функций
влияния относительно функций формы значительно влияет на распре-
деление температуры в теле. В первом варианте (см. рис. 1,
а
) темпе-
ратура выше, чем во втором (см. рис. 1,
б
).
При этом для обоих вариантов с уменьшением характерного раз-
мера
a
уменьшаются и значения температуры. В наноструктурном
Рис. 1. Расположение функции влияния относительно конечного элемента:
1, 2, 3
— соответственно
a
1
, a
2
, a
3
28
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3


