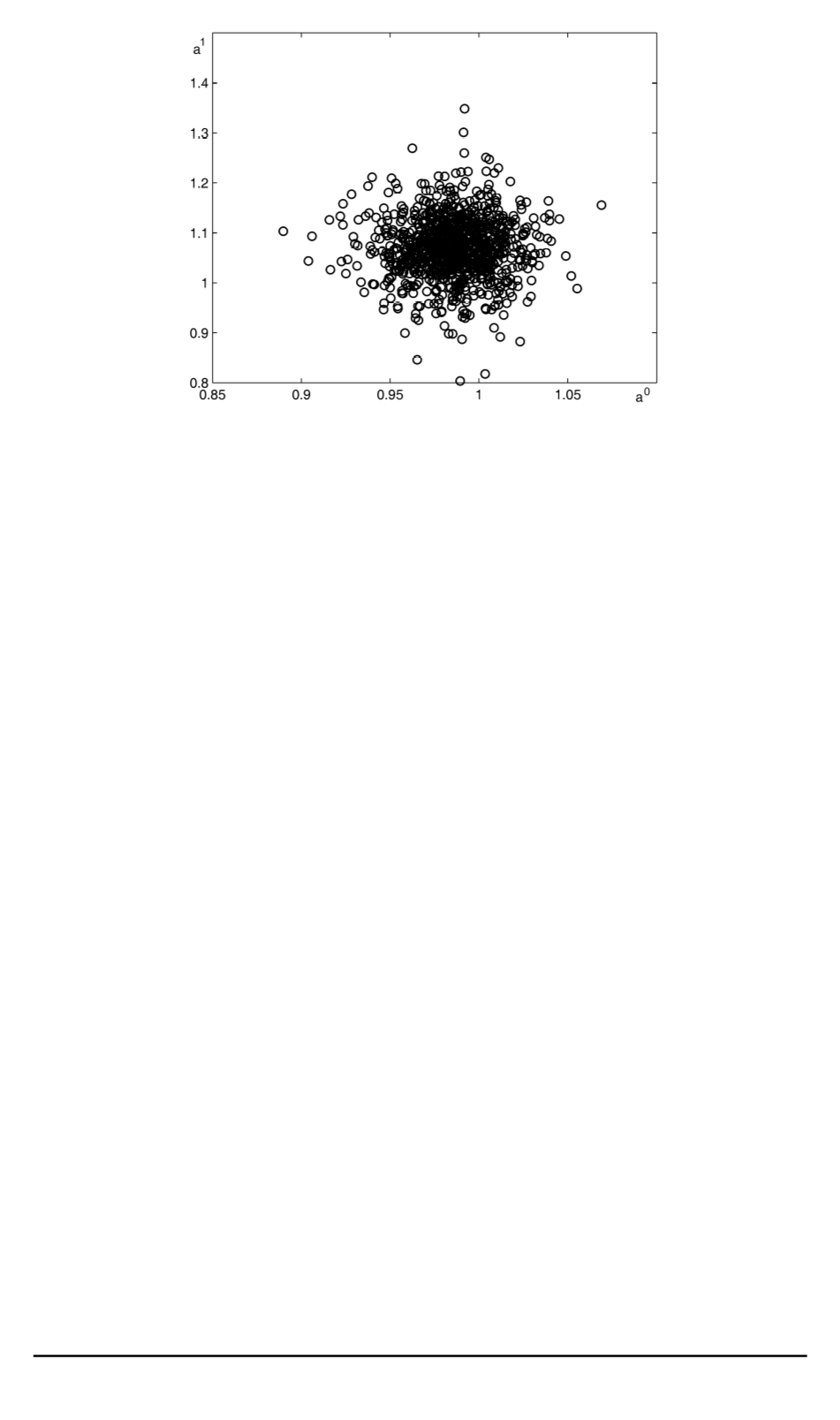
Рис. 5. Случайные реализации оценок
ˆ
a
0
ˆ
a
ˆ
a
и
ˆ
a
1
ˆ
a
ˆ
a
Далее с использованием генератора случайных чисел были полу-
чены случайные реализации оценок
ˆ
a
0
и
ˆ
a
1
, распределенные по зако-
ну Стьюдента. Параметры распределений заданы соотношениями (17)
и (21).
Результаты моделирования представлены на рис. 5, и по ним по-
лучены следующие оценки вероятностей реализации описанных вы-
ше трех сценариев: для первой области
p
1
= 0
,
076
, для второй —
p
2
= 0
,
670
, а для третьей —
p
3
= 0
,
254
.
Заключение.
Проведенные исследования показали возможность
использования разработанной модели для качественного анализа ди-
намики селективного размножения популяции аномальных клеток.
Сравнение результатов моделирования с экспериментальными дан-
ными показывают, что полученные расчетные сценарии развития по-
пуляции соответствуют сценариям, реализующимся в эксперименте,
на относительно небольшом интервале времени и лишь качественно
отражают поведение популяций. Так, неограниченный рост численно-
сти в условиях ограниченного пространства и ограниченного питания
невозможен.
Для более точного соответствия математической модели реально-
му процессу необходимо в дальнейшем учесть плотностной фактор,
т.е. изменение количества клеток в единице объема при изменении
численности популяций, что приводит к изменению вероятностей пе-
рехода в различные состояния.
Работа выполнена при финансовой поддержке Российского фонда
фундаментальных исследований, проект №09–04–00948a, и проекта
№ 2.1.1/227 аналитической ведомственной целевой программы “Раз-
витие научного потенциала высшей школы (2009–2010 годы)”.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3
41


