посаженных клеток. Тогда система (3) примет вид
dx
dt
= (
a
0
−
1)
х
, t >
0;
dy
dt
=
μ
((
a
1
−
1)
y
+
b
1
x
)
, t >
0;
x
(0) = 1;
y
(0) = 0
,
(4)
где коэффициент
μ
=
τ
0
/τ
1
характеризует отношение скоростей раз-
множения аномальных и нормальных клеток.
Решение задачи Коши (4) находим стандартными методами [4]:
x
(
t
) =
e
(
a
0
−
1)
t
, t
≥
0;
y
(
t
) =
μb
1
ϕ
(
e
(
a
0
−
1)
t
−
e
μ
(
a
1
−
1)
t
)
, ϕ
6
= 0
, t
≥
0;
μb
1
te
(
a
0
−
1)
t
, ϕ
= 0
, t
≥
0
,
(5)
где
ϕ
=
a
0
−
1
−
μ
(
a
1
−
1)
.
Проведем параметрический анализ полученных решений.
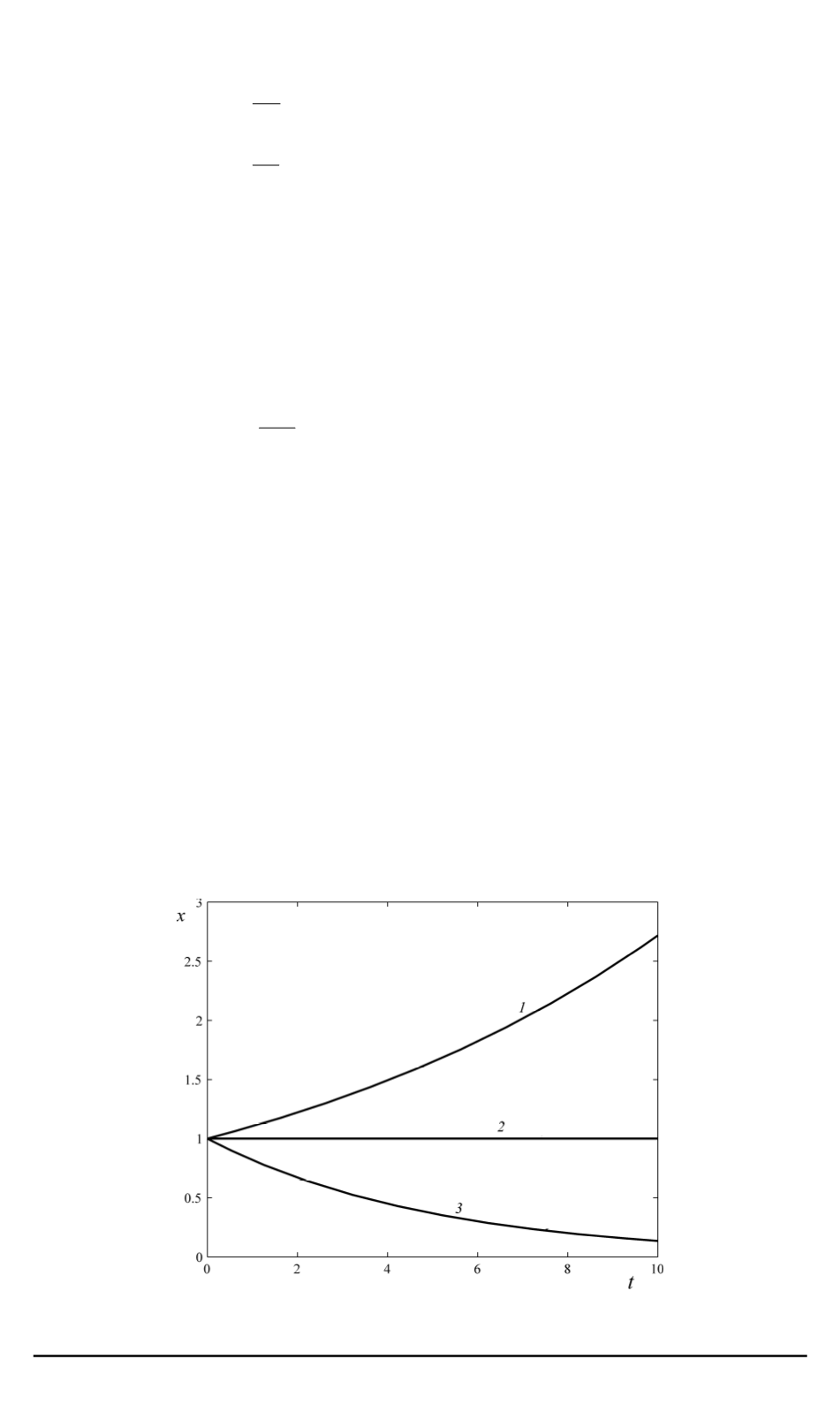
На рис. 1 приведены графики возможного изменения суммарной
численности популяции нормальных клеток (переменной
x
) от време-
ни
t
. Здесь кривая
1
соответствует случаю, когда
a
0
>
1
, кривая
2
—
случаю, когда
a
0
= 1
, а кривая
3
— случаю
a
0
<
1
.
На рис. 2 приведены графики возможного изменения суммарной
численности популяции аномальных клеток (переменной
y
) от време-
ни
t
при
ϕ
= 0
. Здесь кривая
1
соответствует случаю, когда
a
0
>
1
,
кривая
2
случаю, когда
a
0
= 1
, а кривая
3
— случаю
a
0
<
1
. На кривой
3
имеем точку
t
= 1
/
(1
−
a
0
)
,
y
=
b
1
μ/
(1
−
a
0
)
e
.
Рис. 1. Изменение суммарной численности популяции нормальных клеток
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3
33


