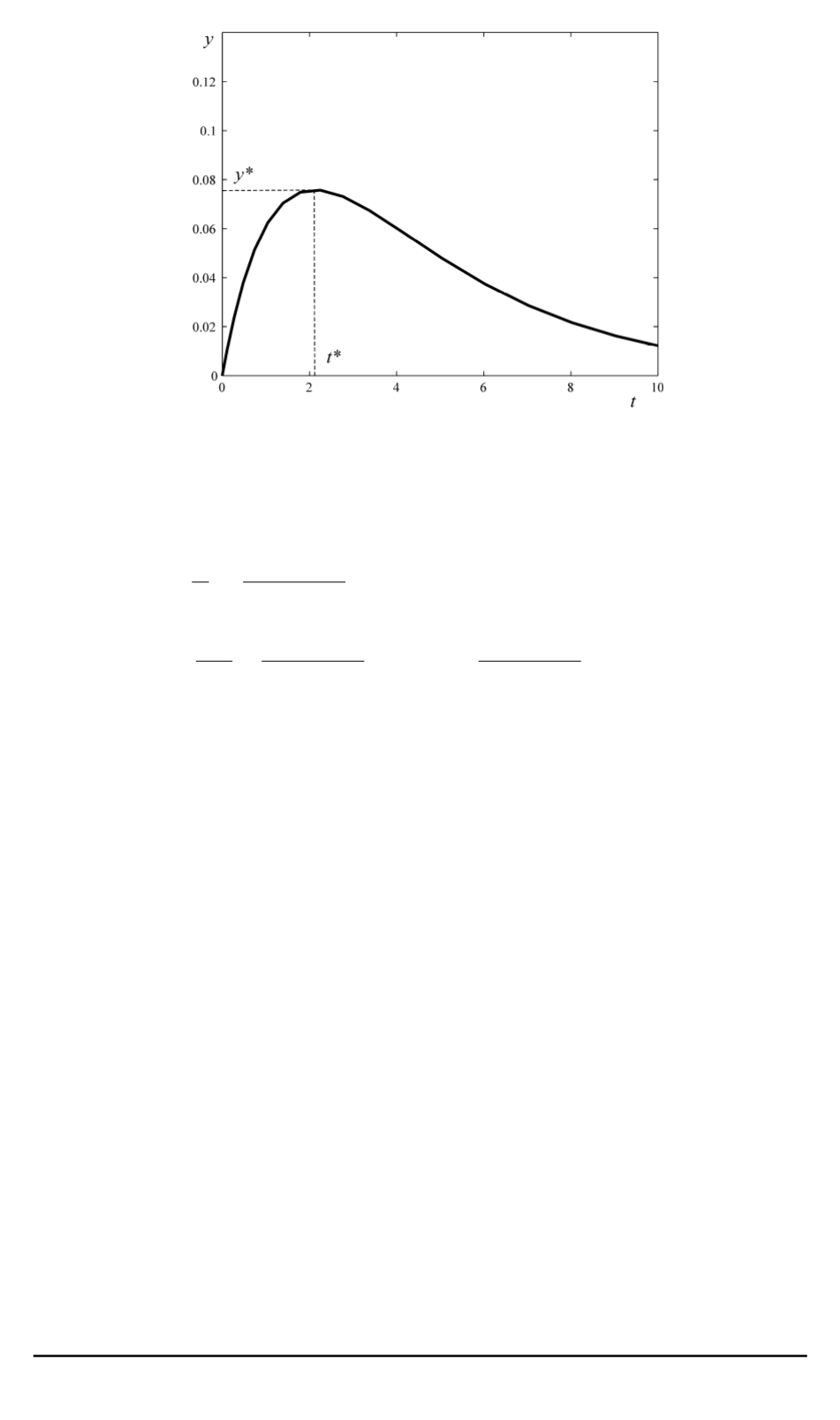
Рис. 4. Изменение суммарной численности популяции аномальных клеток при
a
0
<
1
и
a
1
<
1
,
a
0
6
=
a
1
6
6
t
при
a
0
<
1
и
a
1
<
1
,
a
0
6
=
a
1
. При этом
t
=
1
ϕ
ln
(
a
1
−
1)
μ
a
0
−
1
;
y
=
b
1
μ
ϕ
(
a
1
−
1)
μ
a
0
−
1
(
a
0
−
1)
/ϕ
−
(
a
1
−
1)
μ
a
0
−
1
(
a
1
−
1)
μ/ϕ
!
.
Таким образом, характер динамики суммарных численностей по-
пуляций нормальных и аномальных клеток, образующих изучаемую
популяционную систему, полностью определен значениями параме-
тров
a
0
и
a
1
, входящих в математическую модель (1) и определяемых
равенствами (2), а значение параметра
b
1
определяет максимальные
значения переменной
y
в тех случаях, когда ее изменение ограничено.
В случае, если
μ
= 1
, можно выделить три области значений пара-
метров
a
0
и
a
1
, при которых реализуются различные сценарии. Пер-
вая область задается неравенствами
0
≤
a
0
<
1
и
0
≤
a
1
<
0
, вторая
область — неравенствами
0
≤
a
0
<
1
и
a
1
>
1
, а третья — неравенством
a
0
>
1
.
В первой области с течением времени численность обоих популя-
ций стремится к нулю. Во второй области численность нормальных
клеток стремится к нулю, а численность аномальных — возрастает. В
третьей области растет численность обеих популяций.
Вернемся к рассмотрению дискретной модели (1) и положим
τ
0
=
τ
1
. Перейдем к нормализованным переменным
x
=
X/X
0
,
y
=
Y/X
0
, где
X
0
— число посаженных клеток. Тогда
x
(0) = 1
,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3
35


