
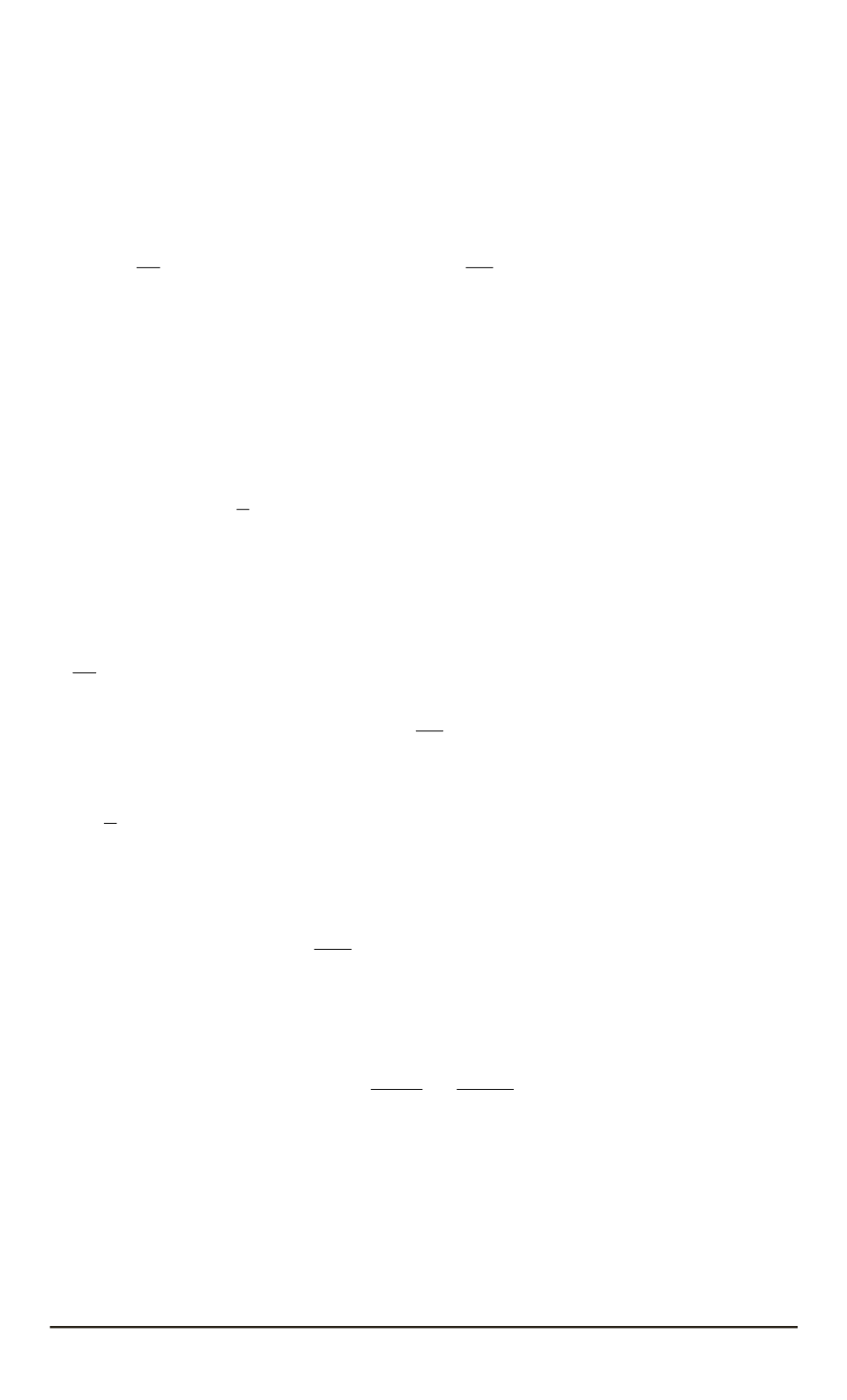
×
10
−
27
эрг
∙
с — постоянная Планка,
˜
k
= 1
,
3807
∙
10
−
16
эрг
/
K — по-
стоянная Больцмана,
T
(
t, x
)
— температура вещества, K. Отметим,
что уравнение (2) записано в предположении локального термоди-
намического равновесия, которое хорошо выполняется в областях,
непосредственно прилегающих к дискам.
3.
Уравнение изменения импульса системы вещество–излучение
∂
∂t
(
ρv
+
G
) +
∇ ∙
b
Π +
b
T
=
1
4
π
(
∇ ×
B
)
×
B
+
F
g
,
(3)
где
G
— плотность импульса излучения, г
/
(
с
∙
см
2
)
,
G
=
W/c
2
;
W
— поток энергии излучения (вектор Пойнтинга), эрг
/
(
с
∙
см
2
)
,
W
=
Z
Ω
ωI dω
;
b
Π
— тензор плотности потока импульса вещества,
г/(см
∙
с
2
),
Π
ij
=
pδ
ij
+
ρv
i
v
j
,
δ
ij
— символ Кронекера,
p
— давление
плазмы, г/(см
∙
с
2
);
b
T
— тензор плотности потока импульса излучения,
г/(см
∙
с
2
),
T
ik
=
1
c
Z
Ω
ω
i
ω
k
I dω
,
c
= 3
∙
10
10
см/с — скорость света;
B
= [
B
1
, B
2
, B
3
]
т
— вектор индукции магнитного поля, Э;
F
g
—
объемная плотность гравитационной силы, дин/см
3
.
4.
Уравнение изменения энергии системы вещество–излучение
∂
∂t
(
e
+
U
) +
∇ ∙
(
v
(
e
+
p
) +
W
) =
=
1
4
π
((
∇ ×
B
)
×
B
)
∙
v
+
F
g
∙
v,
(4)
где
e
,
U
— плотности энергии вещества и энергии излучения, г/(см
∙
с
2
),
U
=
1
c
Z
Ω
Idω
.
5.
Закон Фарадея изменения магнитного поля
(для идеально элек-
тропроводной среды)
∂B
∂t
=
∇ ×
(
v
×
B
)
.
(5)
6.
Уравнение состояния совершенного газа
p
=
ρε
(
γ
−
1)
, где
ε
—
удельная внутренняя энергия, эрг/г;
γ
— показатель адиабаты. Тогда
e
=
ρ
|
v
|
2
2
+
p
γ
−
1
.
(6)
Значение температуры вещества можно получить из соотношения
p
=
n
˜
kT
, где
n
— объемная концентрация вещества.
Наибольшую трудность при решении системы представляет УПИ
(2). Это связано с принципиальной многомерностью этого уравнения,
обусловленной зависимостью искомой функции
I
от направления рас-
пространения. В трехмерном случае при
|
ω
|
= 1
в уравнение (2) вхо-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
77

















