
Следует отметить, что кривые показывают немонотонную зависимость
нормы невязки от числа итераций.
Приведем характерные результаты решения неклассической зада-
чи в условиях, когда функция
ϕ
(
x
)
задана с погрешностью. В экс-
периментах функция
ϕ
(
x
)
, x
∈
ω
, возмущалась следующим образом:
ϕ
δ
(
x
) =
ϕ
+
δσ
(
x
)
,
x
∈
ω,
где
σ
(
x
)
— случайные величины, равномерно
распределенные на отрезке [– 1, 1]. Итерационный процесс сопряжен-
ных градиентов обрывался по достижению нормы невязки значения
δ
, т.е. при
||
r
k
(
δ
)
|| ≤
δ.
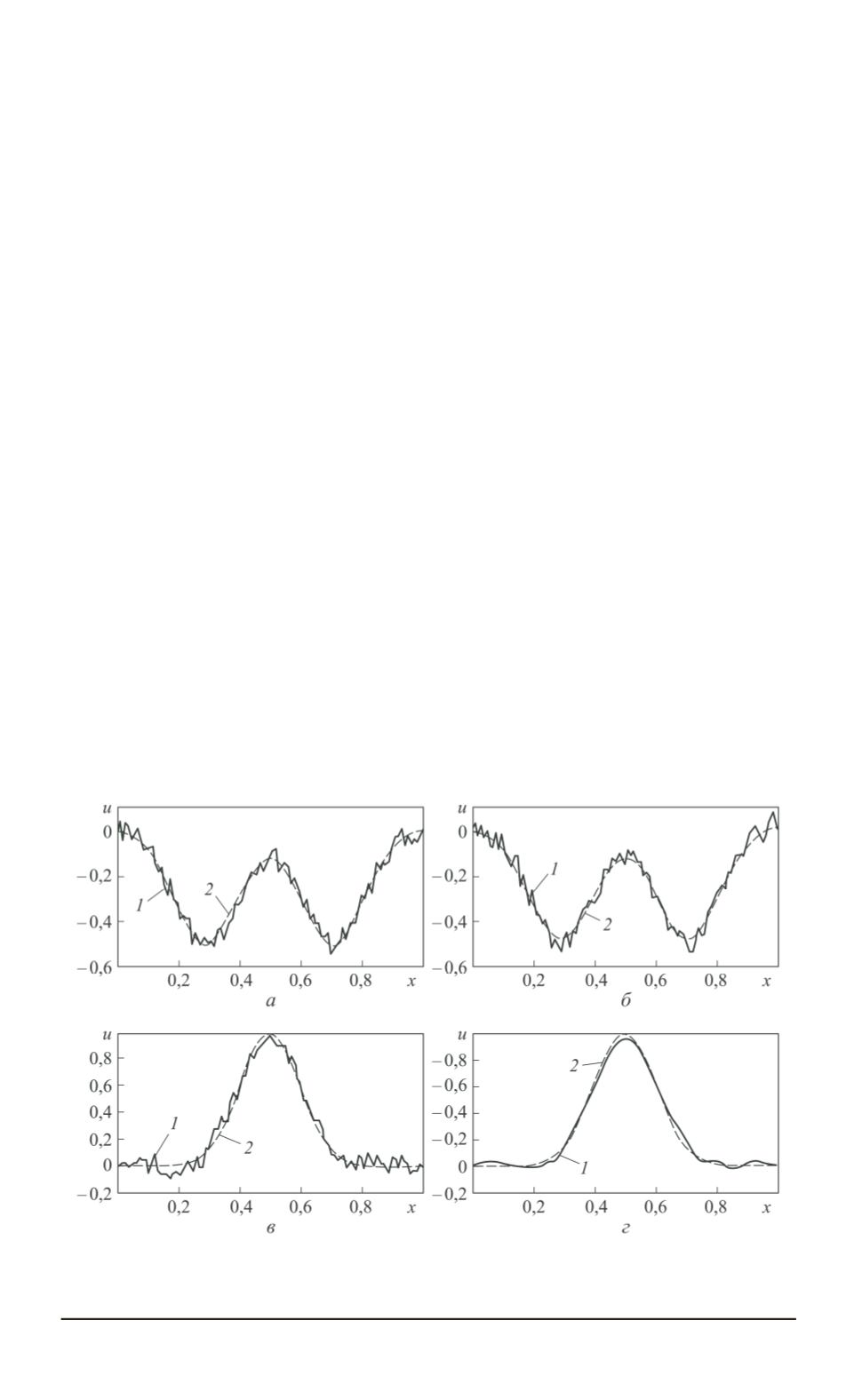
Полученное приближенное решение (кривая
1
)
для уровня погрешности во входных данных, определяемых величи-
ной
δ
= 0
,
05
(20%), и исходная функция
ϕ
(
x
)
(кривая
2
) приведены
на рис. 3,
а
. Найденная сеточная функция
ϕ
(искомое начальное усло-
вие) и точное начальное условие (кривая
2
) представлены на рис. 3,
в
.
Согласно этим зависимостям, искомое начальное смещение струны
найдено с сохранением начального уровня возмущений.
Для выделения более гладкого решения, принадлежащего вместо
пространства
L
2
(
ω
)
сеточному пространству
W
1
2
(
ω
)
, зададим сглажи-
вающий оператор
D
ϕ
=
−
5
ϕ
ˉ
xx
+
ϕ, x
∈
ω
, в виде сеточных функций,
обращающихся в нуль в граничных узлах.
Возмущенный вариант входящей функции
ϕ
δ
(
x
)
(кривая
1
) и функ-
ция
ϕ
(
x
)
(кривая
2
), которая определена в результате сглаживания
функции
ϕ
δ
(
x
)
, приведены на рис. 3,
б
. Искомое точное решение (кри-
вая
2
) и решение полученное с помощью предлагаемого итерационно-
го процесса (кривая
1
) представлены на рис. 3,
г
. Здесь даны результа-
ты расчета на пространственной сетке
M
= 100
,
h
= 0
,
01
с помощью
Рис. 3. Характерные результаты решения неклассической задачи в условиях,
когда функция
ϕ
δ
(
x
)
задана с погрешностью
84
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















