
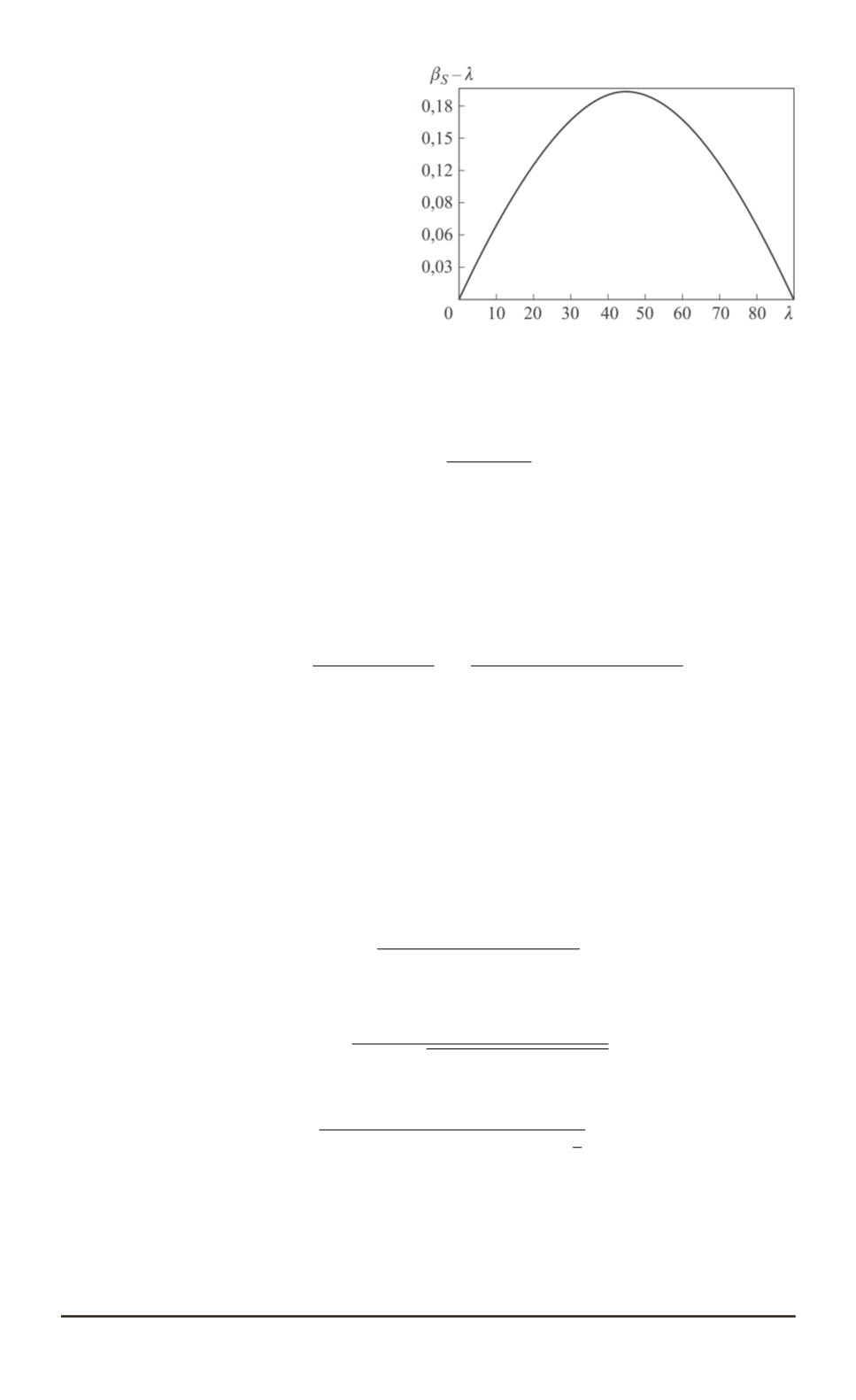
Рис. 2. Зависимость разности
β
S
−
λ
от
параметра
λ
, построенная по форму-
ле (16)
где
Θ
go
— гринвичское сред-
нее сидерическое время (GMST)
при
t
О
;
ω
⊕
— угловая ско-
рость Земли. Напомним, что ось
OX
направлена в точку встречи
гринвичского меридиана с эква-
тором, поэтому
Θ
go
= 0
.
Угол
β
S
между линией, со-
единяющей точку
O
0
с точкой
S
(см. рис. 1), и экваториальной
плоскостью принимают за гео-
дезическую широту [10, 22]
β
S
= tg
−
1
tg
λ
(1
−
f
)
2
,
(15)
где
f
= 1
/
298
,
2947
— фактор сжатия Земли. Предыдущее предположе-
ние приведет к возникновению погрешности значения
δβ
(см. рис. 1).
Если эту погрешность игнорировать, то отличие геоцентрической ши-
роты
λ
от геодезической
β
S
можно найти как
tg (
β
S
−
λ
) =
tg
β
S
−
tg
λ
1 + tg
λ
=
2
f
−
f
2
(1
−
f
)
2
(1 + 1
/
tg
λ
)
.
(16)
В этом случае отличие геоцентрической широты от геодезической
зависит только от параметра
λ
. Зависимость разности
β
S
−
λ
от па-
раметра
λ
приведена на рис. 2. Наибольшее отличие геодезической
широты от геоцентрической достигается на широте 45
◦
и составляет
β
S
−
λ
∼
= 0
,
1921
◦
∼
= 11
,
315
0
.
Для получения более точных результатов угол
δβ
можно вычислить
по формуле
δβ
= tg
−
1
H
sin (
β
S
−
λ
)
ρ
a
+
H
cos (
β
S
−
λ
)
,
(17)
где
H
=
|
r
| −
b
e
cos
λ
p
(tg
λ
)
2
+ (1
−
f
)
2
;
(18)
ρ
a
=
a
e
(1
−
f
)
2
h
1
−
(2
f
−
f
2
)(sin
β
S
)
2
i
3
2
;
(19)
|
r
|
— модуль вектора положения
r
спутника. Уравнение (19) — уравне-
ние радиуса кривизны в меридиональном направлении. В этом случае
отличие геоцентрической широты
λ
от геодезической
β
зависит от
108
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4

















