
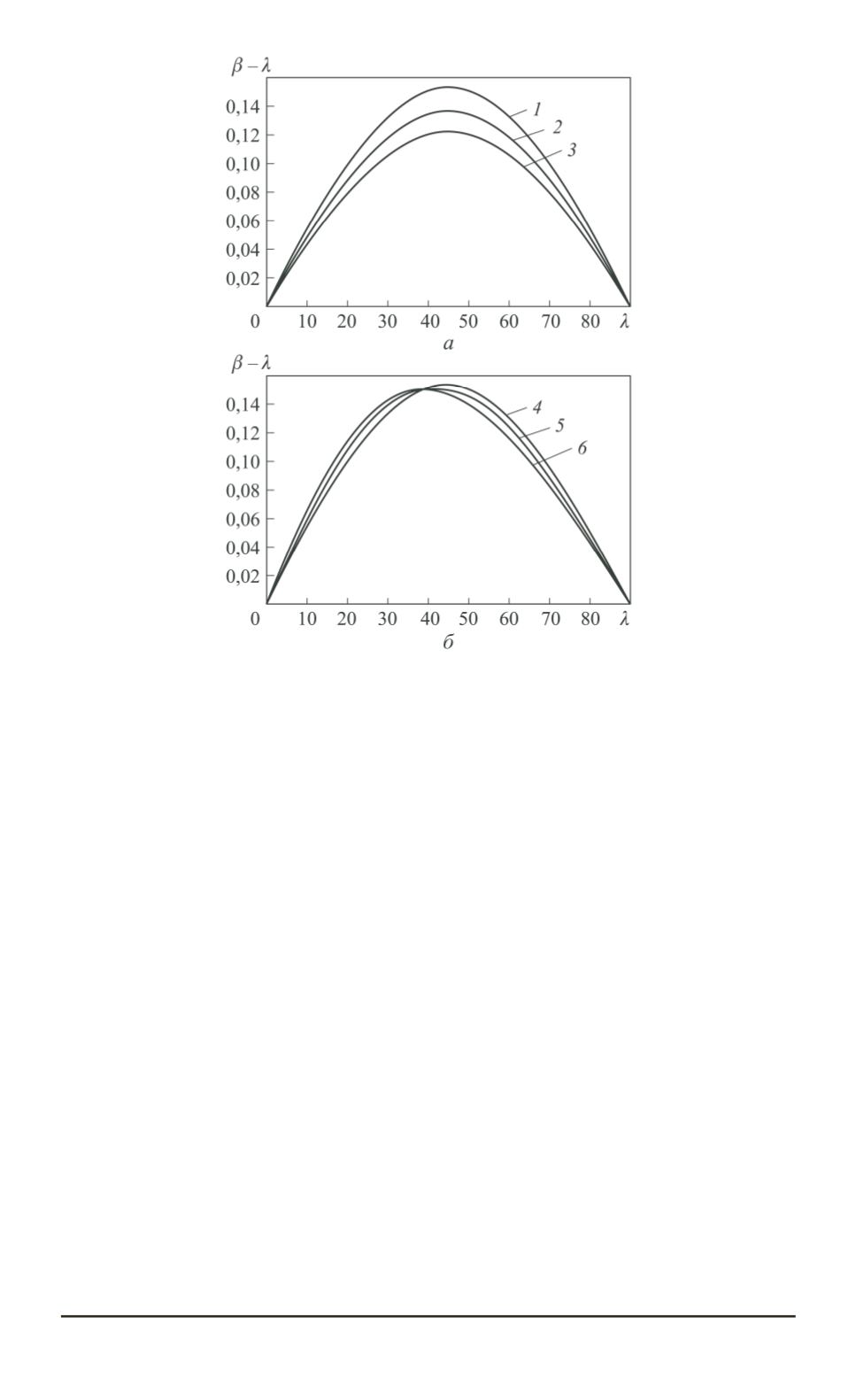
Рис. 3. Зависимость разности
β
−
λ
от параметра
λ
при значениях вектора
положения
r
= 8 000
(
1
), 9 000 (
2
), 10 000 (
3
) (
а
), построенная по формуле (20),
и то же при значениях эксцентриситета
e
= 0
(
4
), 0,1 (
5
), 0,2 (
6
), построенная
по формуле (26)
шенствовать проекты. Инструмент SIMULINK полностью интегриро-
ван с MATLAB, обеспечивая немедленный доступ к широкому спек-
тру инструментов анализа и проектирования [24]. Предположим, ор-
бита имеет следующие параметры:
а
= 8000
км;
i
= 45
◦
;
ω
= 0
◦
;
e
= 0
,
0
,
1
,
0
,
2; Ω = 20
◦
;
ν
= 0
◦
при
T
= 0
. Путем введения значения
орбитальных параметров в модели получим трассы спутника относи-
тельно геодезической и сферической систем координат. Теперь выяс-
ним, насколько отличаются результаты при неиспользовании сжатого
сфероида. Зависимость разности
β
−
λ
от параметра
λ
при различных
значениях эксцентриситета
e
приведена на рис. 3,
б
. Наибольшее отли-
чие геодезической широты от геоцентрической достигается на широте
45
◦
при
e
= 0
и составляет
β
−
λ
∼
= 0
,
1531
◦
∼
= 9
,
11
0
(21 км).
Согласно распространенному мнению, некоторые из найденных
отличий могут казаться малыми, но это зависит от требований к сле-
жению. В рассматриваемом случае максимальное разрешение данных
в атласах локальных значений альбедо [4–7] составляет
5
◦
×
5
◦
(или
550
×
550
км), поэтому можно утверждать, что эта разность, вызванная
110
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4

















