
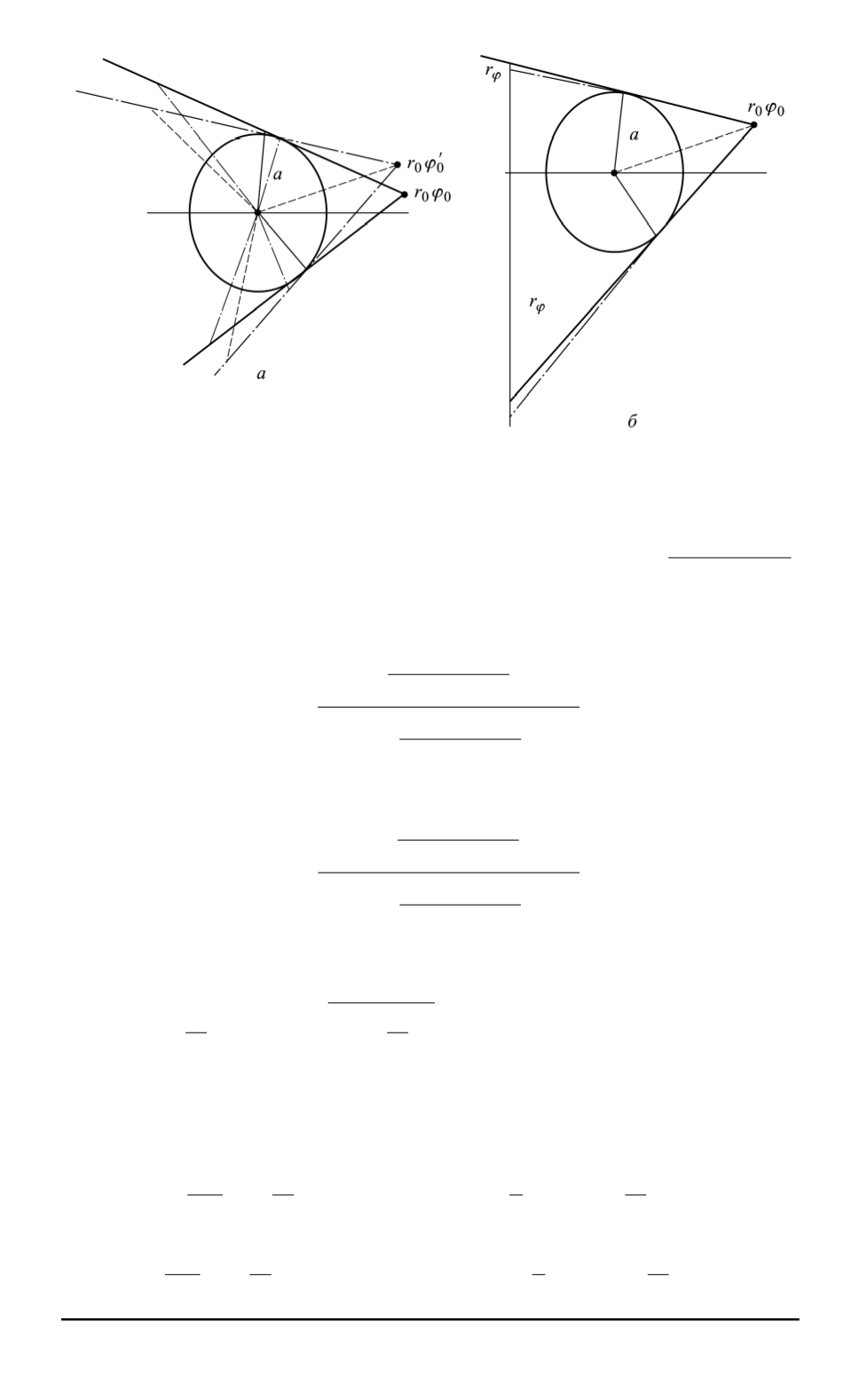
Схемы, иллюстрирующие сдвиг границы свет–тень
прямой
y
=
kx
+
b
на плоскости в декартовых координатах может быть
переписано как уравнение в полярных координатах
r
=
b
sin
−
k
cos
ϕ
.
Легко проверить, что уравнения (25) могут быть преобразованы в урав-
нения прямых (касательных) вида
r
=
a
cos(
ϕ
0
−
β
)
sin
ϕ
−
sin(
ϕ
0
−
β
)
cos(
ϕ
0
−
β
)
cos
ϕ
,
(26)
где в области тени угол
ϕ
принадлежит первому и второму квадрантам;
r
=
−
a
cos(
ϕ
0
+
β
)
sin
ϕ
−
sin(
ϕ
0
+
β
)
cos(
ϕ
0
+
β
)
cos
ϕ
;
(27)
где угол
ϕ
принадлежит третьему и четвертому квадрантам в той же
области, если взять косинус от обеих частей соответствующего равен-
ства. Здесь
a
r
0
= sin
β
;
r
1
−
a
r
0
2
= cos
β
.
Для цилиндра с покрытием соответствующие соотношения для
действительной части показателей экспонент в (23), обеспечивающие
сходимость ряда, записываются в виде
−
k
0
a
6
1
/
3
q
k
2
α
|
ϕ
−
ϕ
0
| −
arccos
a
r
−
arccos
a
r
0
<
0;
−
k
0
a
6
1
/
3
q
k
2
α
(2
π
|
ϕ
−
ϕ
0
|
)
−
arccos
a
r
−
arccos
a
r
0
<
0
,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 5
47
















