
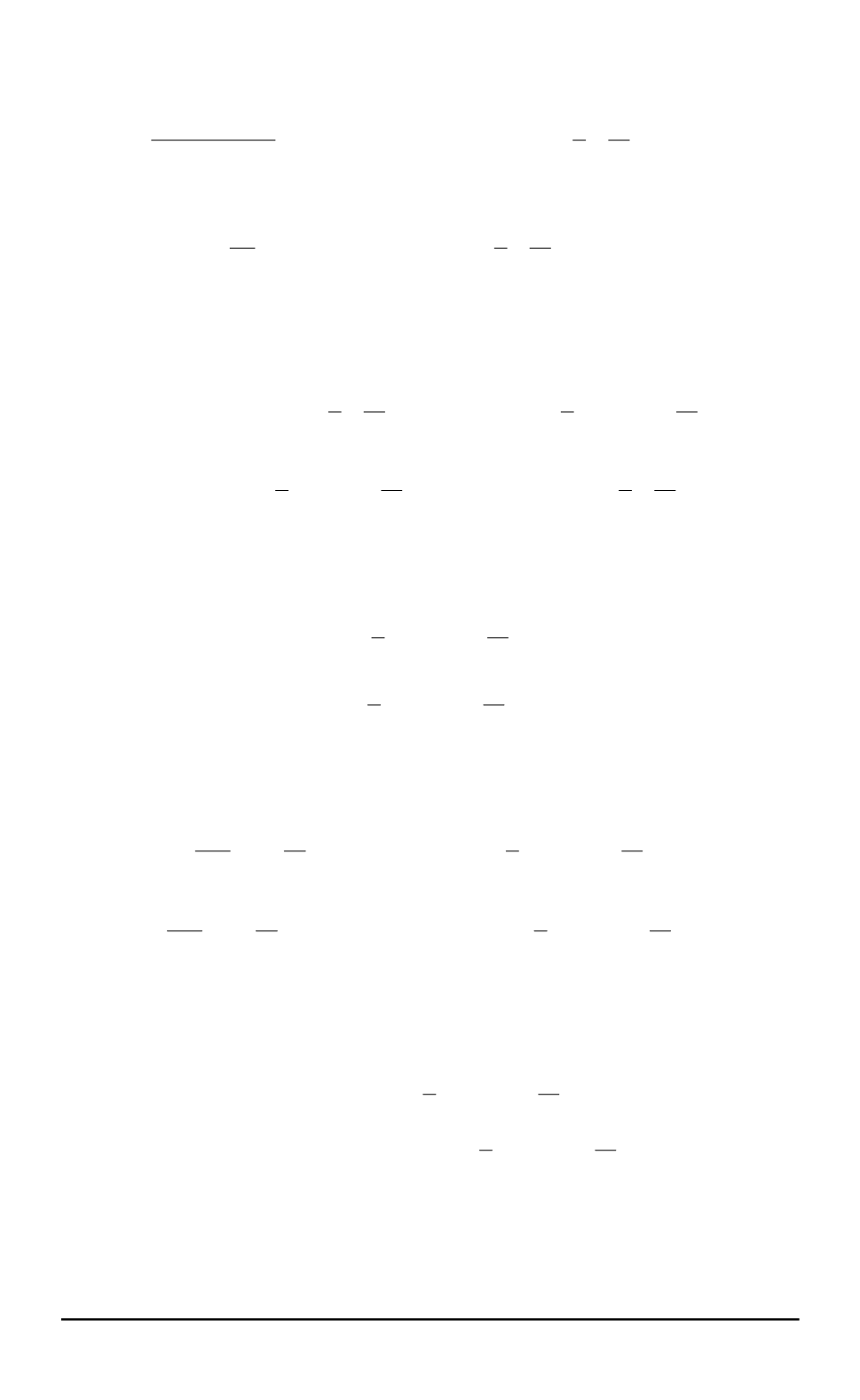
получаем
sgn
(
ϕ
−
ϕ
0
)
μ
k
ϕ
Z
ϕ
0
g
1
/
2
μ
k
(
t
)
dt
≈ |
ϕ
−
ϕ
0
|
1
−
δ
a
ε
ε
0
−
1 ;
1
μ
k
2
π
Z
0
g
1
/
2
μ
k
(
t
)
dt
≈
2
π
1
−
δ
a
ε
ε
0
−
1
.
Выпишем выражение в фигурных скобках из равенства (21) с уче-
том сделанных приближений
exp
iμ
k
|
ϕ
−
ϕ
0
|
1
−
δ
a
ε
ε
0
−
1
−
arccos
a
r
−
arccos
a
r
0
+
+exp
iμ
k
−
arccos
a
r
−
arccos
a
r
0
+ 2
π
−|
ϕ
−
ϕ
0
|
1
−
δ
a
ε
ε
0
−
1
.
(23)
При отсутствии слоя диэлектрика (
ε
=
ε
0
) выражение (23) примет вид
exp
iμ
k
|
ϕ
−
ϕ
0
| −
arccos
a
r
−
arccos
a
r
0
+
+ exp
iμ
k
−
arccos
a
r
−
arccos
a
r
0
+
h
2
π
− |
ϕ
−
ϕ
0
|
i
.
(24)
Для сходимости ряда (24) действительная часть показателей экспо-
нент должна быть отрицательной. Должны выполняться неравенства
−
k
0
a
6
1
/
3
q
k
2
|
ϕ
−
ϕ
0
| −
arccos
a
r
−
arccos
a
r
0
<
0;
−
k
0
a
6
1
/
3
q
k
2
2
π
− |
ϕ
−
ϕ
0
| −
arccos
a
r
−
arccos
a
r
0
<
0
.
Для определенности полагаем, что угол
ϕ
0
принадлежит перво-
му квадранту. При этом геометрическая граница сходимости ряда в
точности совпадает с границей свет–тень
|
ϕ
−
ϕ
0
|
= arccos
a
r
+ arccos
a
r
0
;
|
ϕ
−
ϕ
0
|
= 2
π
−
arccos
a
r
−
arccos
a
r
0
,
(25)
которая состоит из двух касательных, проведенных к окружности ра-
диусом
r
=
a
из точки источника (
r
0
, ϕ
0
). Действительно, равенства
(25) выполняются, если точка наблюдения (
r, ϕ
) принадлежит одной из
таких касательных (часть
а
рисунка). Известно, что уравнение любой
46
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 5
















