
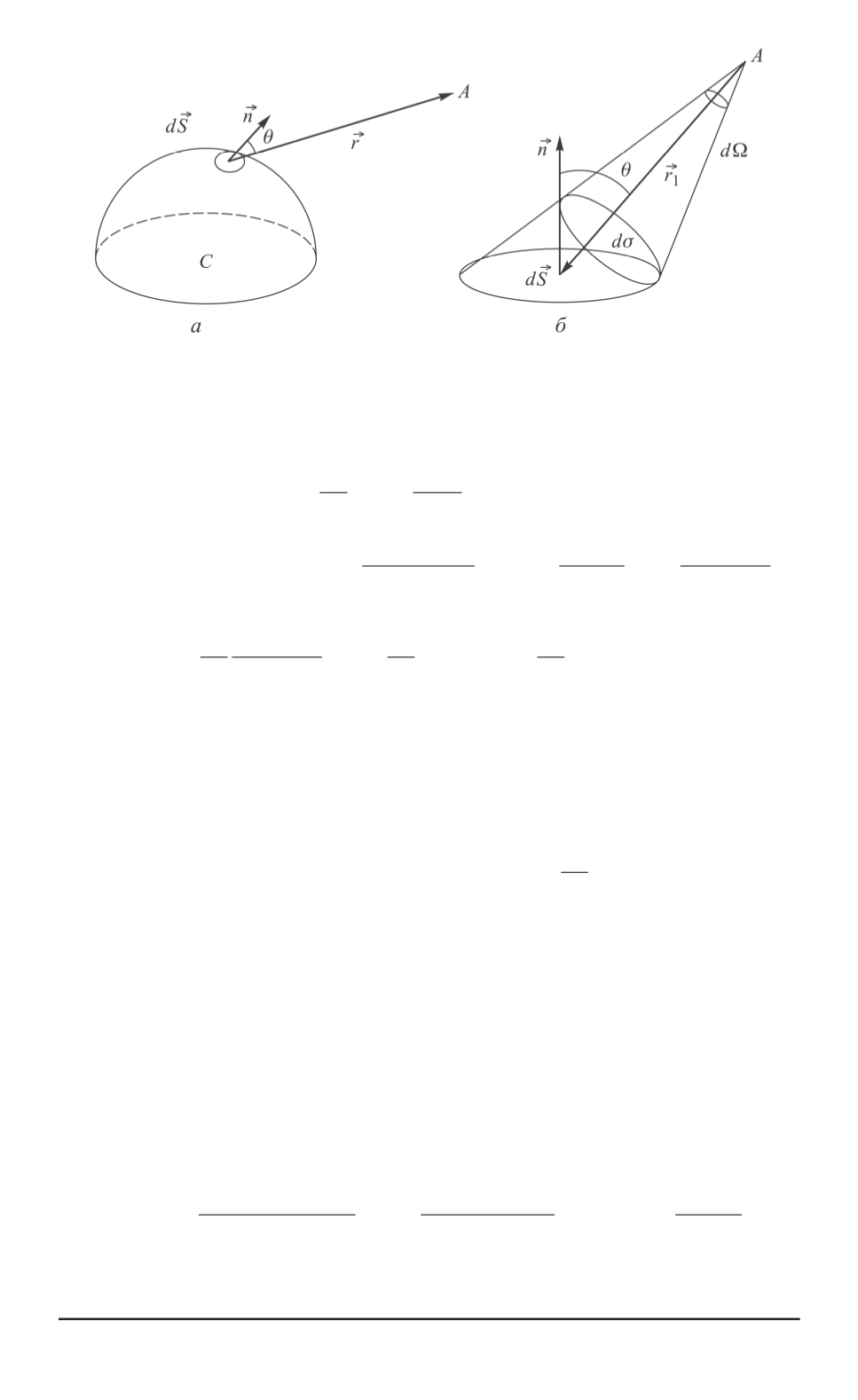
Рис. 4. Схемы к выводу поля магнитной поверхности
поверхности. Следовательно (рис. 4),
dσ
=
dS
cos
θ
;
d
Ω =
dσ
r
2
1
=
dS
cos
θ
r
2
1
=
=
−
dS
cos (
π
−
θ
)
r
2
1
=
−
dS
(
~n, ~r
1
)
r
3
1
=
−
d ~S, ~r
1
r
3
1
.
Тогда
dψ
=
I
4
π
~r
1
, d ~S
r
3
1
=
−
I
4
π
d
Ω
ψ
=
−
I
4
π
Ω
, где
Ω
— телесный
угол, образованный с центром в точке наблюдения и опирающийся
на искомый контур. Таким образом, установлено, что магнитный ска-
лярный потенциал в рассматриваемой задаче не зависит от формы
поверхности, а зависит только от пространственного расположения
ограничивающего поверхность контура. Напряженность магнитного
поля вычисляется стандартно:
~H
=
−∇
ψ
=
I
4
π
∇
Ω
. Для определе-
ния градиента телесного угла воспользуемся следующей процедурой.
Сместим точку наблюдения на некоторый малый вектор
δ~s
и вычи-
слим изменение телесного угла. Из определения градиента можно за-
писать:
d
Ω = (
∇
Ω
, δ~s
)
. Полагая точку наблюдения неподвижной, все
элементы
d~l
контура смещаются на одинаковый вектор
−
δ~s
, причем
каждый из них описывает площадь
d ~S
=
−
h
δ~s, d~l
i
. Следовательно,
изменение телесного угла, связанное с дополнительным изменением
поверхности, на которую опирается этот угол, равно
d
Ω =
−
I
C
−
h
δ~s, d~l
i
, ~r
r
3
=
I
C
h
d~l, ~r
i
, δ~s
r
3
=
δ~s,
I
C
h
d~l, ~r
i
r
3
.
Сравнивая два выражения для малого изменения телесного угла, полу-
34
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
















