
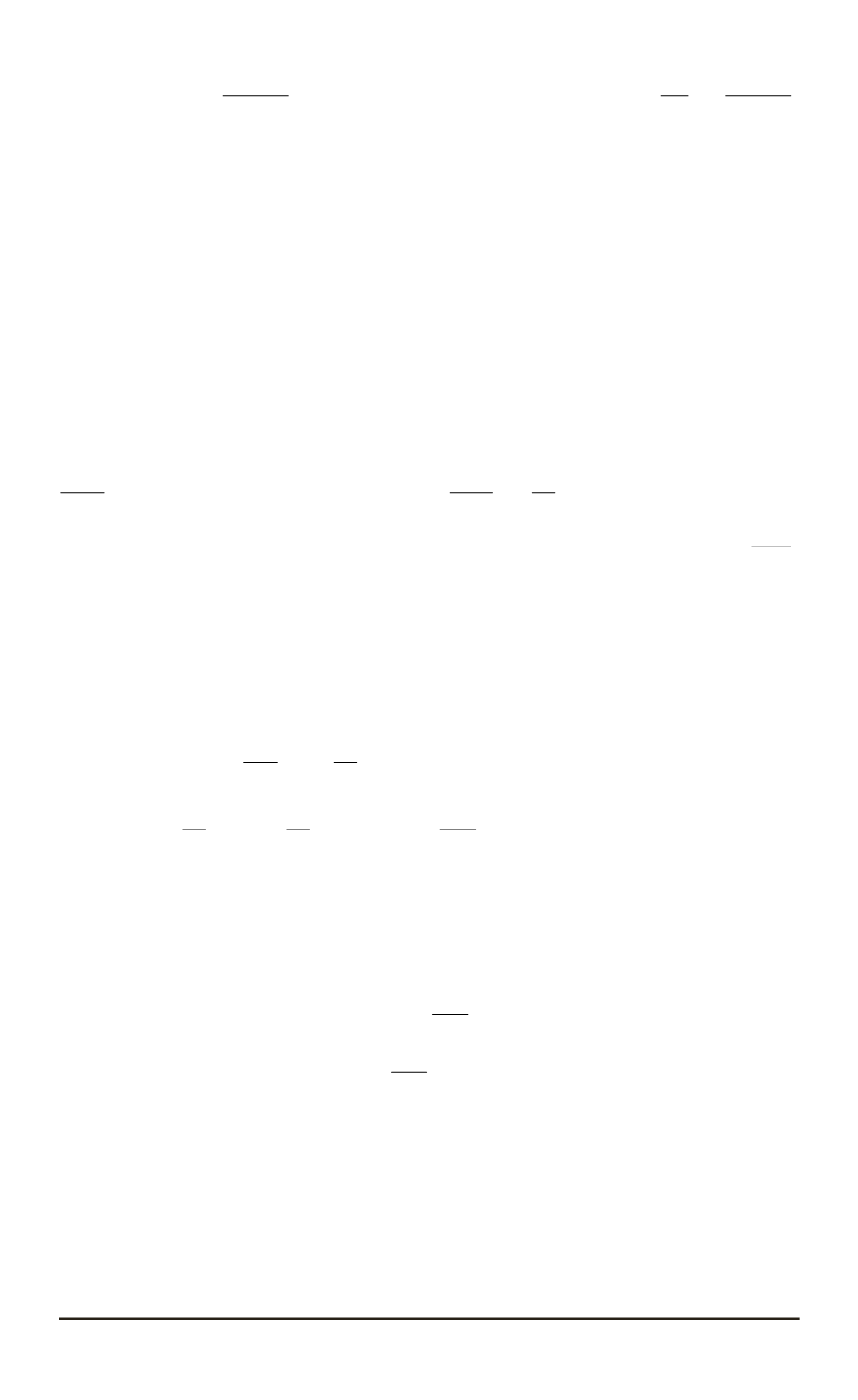
чаем:
∇
Ω =
I
C
h
d~l, ~r
i
r
3
. Откуда запишем выражение
~H
=
I
4
π
I
C
h
d~l, ~r
i
r
3
,
согласно которому полученное магнитное поле поверхности можно
определить по закону Био-Савара, полагая, что ток
I
протекает по
замкнутой кривой, на которую опирается рассматриваемая поверх-
ность, причем направление тока и внешней нормали согласованы.
Выше были рассмотрены некоторые задачи магнитостатики. Мо-
дифицируем уравнения Максвелла, включив в них объемную плот-
ность и плотность тока магнитных зарядов. Как было отмечено, объ-
емная плотность магнитных зарядов связана с намагниченностью со-
отношением
ρ
m
=
−
div
~M
. Примем, что для магнитных зарядов по
аналогии с электрическими выполняется уравнение непрерывности
∂ρ
m
∂t
+
div
~j
m
= 0
. Тогда
div
~j
m
=
−
∂ρ
m
∂t
=
∂
∂t
div
~M,
откуда с точно-
стью до несущественного постоянного слагаемого имеем
~j
m
=
∂ ~M
∂t
.
Последнее соотношение можно полагать определением плотности то-
ка магнитных зарядов. Таким образом, можно преобразовать систему
уравнений Максвелла к виду
0 = div
~B
= div
μ
0
~H
+
~M
; div
~H
=
−
div
~M
=
ρ
m
;
rot
~E
=
−
∂ ~B
∂t
=
−
∂
∂t
h
μ
0
~H
+
~M
i
=
=
−
∂
∂t
μ
0
~H
−
∂
∂t
μ
0
~M
=
−
μ
0
∂ ~H
∂t
−
μ
0
~j
m
.
Окончательно запишем полную систему уравнений
div
~H
=
ρ
m
;
div
~D
=
ρ
e
;
rot
~E
=
−
μ
0
∂ ~H
∂t
−
μ
0
~j
m
;
rot
~H
=
∂ ~D
∂t
+
~j
e
.
Для того чтобы записать полученную систему в терминах комплекс-
ного векторного поля необходимо разобраться в динамике поляризо-
ванных зарядов. Запишем соотношения, связывающие электрическое
смещение и объемную плотность связанных зарядов с поляризован-
ностью
div
~P
=
−
ρ
p
,
~D
(
~r
) =
ε
0
~E
(
~r
) +
~P
(
~r
)
, и подставим их в полу-
ченную систему
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
35
















