
определена в виде
f
(
x
) =
3
X
i
=1
γ
i
f
2
i
(
x
) +
α
k
x
k
2
2
, где
γ
i
, f
i
(
x
)
— весовой
коэффициент и частный критерий, соответствующие
i
-й собственной
частоте,
f
i
(
x
) = (
ω
∗
i
−
ω
i
(
x
))
,
i
= 1
,
3
;
x
∈
R
2
.
При решении использован гибридный алгоритм M-PCASFC [20].
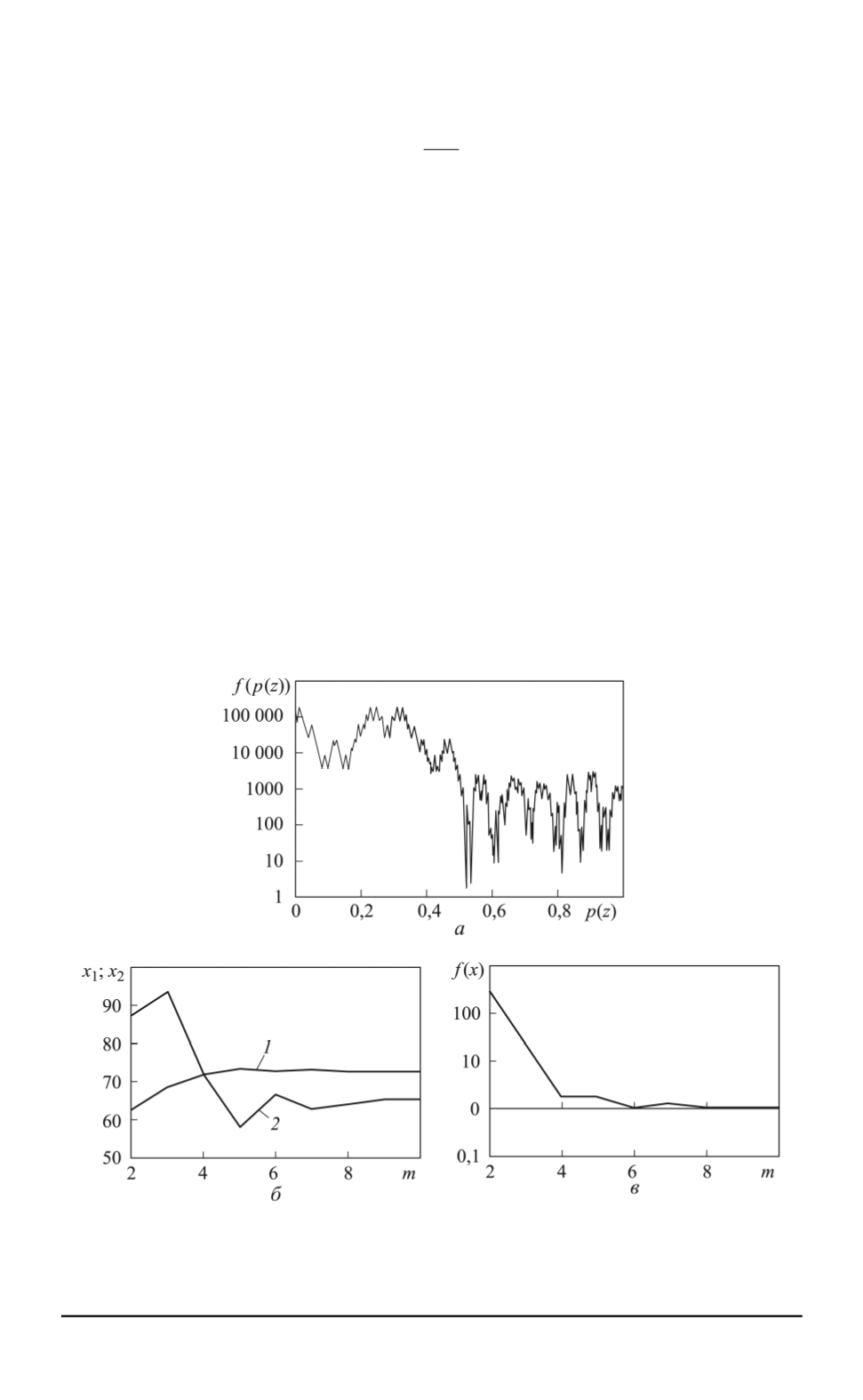
Изменение значений одномерной критериальной функции
f
(
p
(
z
))
показано на части
а
рисунка: глобальный минимум функции, соот-
ветствующий заданной плотности развертки
m
= 5
кривой Пеано,
f
(
z
∗
)
≈
0
,
16968
∙
10
1
определен при
z
∗
≈
0
,
535156
. Зависимости пере-
менных управления и критериальной функции от плотности развертки
кривой Пеано представлены на частях
б
и
в
рисунка; глобальный ми-
нимум функции
f
(
z
∗
)
≈
0
,
96811
реализован для
m
= 10
; при этом
значениям переменных управления
x
10
1
≈
72
,
705
%,
x
10
2
≈
65
,
674
%
соответствуют плотность жидкости
1091
кг/м
3
и скорость течения
26
,
27
м/с. Следует отметить, что наибольшая относительная погреш-
ность, соответствующая здесь восстановленному значению скорости
потока, не превышает 0,9%. Можно констатировать хорошую согла-
сованность полученного приближенного решения модельной задачи,
обусловленного в том числе выбором значений параметра регуляри-
зации, и заданной входной информации.
Изменение значений одномерной критериальной функции
f
(
p
(
z
))
на единичном
интервале (
а
), зависимость переменных управления
x
1
(
1
),
x
2
(
2
) от плотности
развертки
m
кривой Пеано (
б
), зависимость критериальной функции
f
(
x
)
от
плотности развертки
m
кривой Пеано (
в
)
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2016. № 2
















