
58
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. «Естественные науки». 2016. № 3
Введение.
В последнее время в связи с раз-
витием ракетной космической техники общего
машиностроения в значительной степени возрос
интерес к исследованию динамики сложных
жидкостей [1]. Одной из используемых моделей
подобной жидкости может являться дискретно-
стратифицированная жидкость, представляю-
щая собой совокупность слоев несмешиваю-
щихся несжимаемых жидкостей. Колебаниям
стратифицированных и несмешивающихся
жидкостей посвящено достаточно много работ
(например, [2–11]).
В настоящей статье рассмотрены колеба-
ния трех идеальных жидкостей, каждая из ко-
торых совершает несжимаемое движение. По-
лучены дифференциальные уравнения для
обобщенных координат, отражающих колеба-
ния поверхностей раздела жидкостей, и пред-
ложены эквивалентные механические маятни-
ковые модели, моделирующие колебания жид-
костей по
n
-му тону.
Постановка задачи.
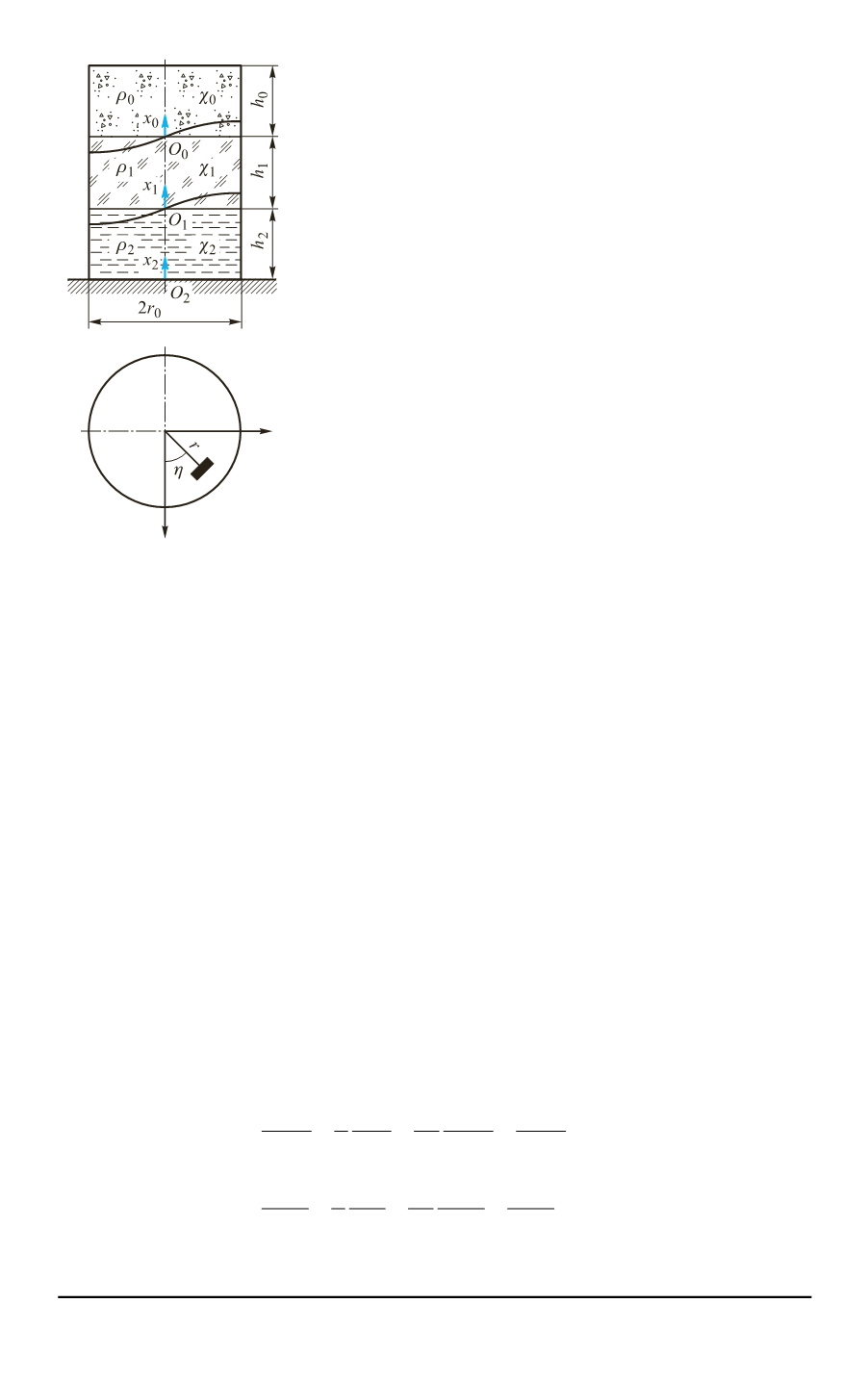
Рассмотрим систему
из трех невязких несжимаемых и несмешива-
ющихся жидкостей, полностью заполняющих
цилиндрический сосуд. Введем цилиндриче-
ские системы координат
,
i i
O x r
0, 1, 2,
i
с началами координат, рас-
положенными на поверхностях разделов жидкостей и на дне (рис. 1).
Обозначим плотность и глубину каждого слоя жидкости через
ρ ,
,
0, 1, 2,
i
i
i h
соответственно. При решении задачи примем следу-
ющие допущения:
−
перемещения и скорости всех частиц жидкостей — малые вели-
чины, т. е. произведениями и квадратами можно пренебречь по срав-
нению со значениями любой из этих величин;
−
движение каждой жидкости является потенциальным.
Вследствие сделанных допущений колебания трех жидкостей могут
быть описаны уравнениями Лапласа для потенциалов смещений частиц
жидкостей в цилиндрической системе координат [12]:
2
2
2
0
0
0
0
2
2 2
2
0
2
2
2
1
1
1
1
2
2 2
2
1
1
1
0;
1
1
0;
r r r r
x
r r r r
x
(1)
Рис. 1.
Схема системы,
состоящей из трех невяз-
ких несжимаемых и не-
смешивающихся жидко-
стей, полностью запол-
няющих цилиндрический
сосуд
















